Excerpt
— juodoji 142 Genys 120 Gervė 145 Grąžiagalvė 154 Guiros 142 Gulbės 150 — nebylė 114 Jerubė 120, 131 Kalakutas 189 Kalviukas dirvoninis 182 Karveliai 10, 63, 73, 78, 86, 129, 143, 144, 162, 172, 185, 209 Kėkštas 150 Kielė 186 Kikiliai 89, 95, 171, 172, …
Excerpt
Hominidai 5, 9, 194, 203 Hominoidai 194 Homo erectus 195 — habilis 195 — sapiens 195 Kapucinai 86 Kromanjoniečiai 195 Lemūrai 86, 114, 160 Markatos 86 — žaliosios 160 Neandertaliečiai 195, 200 Orangutanas 30, 120, 195 Paleantropai 197, 200 Pavianai 84, …
Excerpt
Būrys. Neporakanopiai (Perissodacty- la) =— 75, 111, 120, 129 Arkliai 24, 109, 136, 156, 181 — torpanai 132, 145 Asilas 24 Raganosiai 182 Zebras 156 Būrys. Porakanopiai (Artiodactyla) =— 75, 109, 111, 113, 129, 133, 182 Antilopės 4, 142, 161 Avijautis 142 …
Excerpt
TURINYS Pratarmė 3 I skyrius. Įvadas || kaka kia a kaka aaa aaa aaa aaa akis 3 1. Zoopsichologijos dalykas ........... 3 2. Zoopsichologijos metodai 11 3. Zoopsichologijos istorija 22 I! skyrius. Pagrindi elgsenos komponentai 36 1. Taksiai ir kinezės …
Excerpt
Bagdonas A. Ba-119 Zoopsichologija: Vadovėlis respublikos aukšt. m-klų psi- chologijos spec. studentams.-— V.: Mokslas, 1983.— 223 p., iliustr. Bil:liogr.: p. 205—213. Rodyklės: p. 214—222. Vadovėlyje apiltūdinamas zoopsicholozijos objektas, jos ryšys su …
Excerpt
vu BIBLIOTEKA. RPI 324 …
Excerpt
——- ——— p „L 4 I 8 D B ) 8, C C '0 64 pav. Trijų spalvų maišymo schema (Lindsė- jus ir Normanas, 1974 j. Paaiškinimai tekste. sime spalvą El, Ly. nedidelio sodrumo spalvą E (64 pav., I). Paėmę kitokį pirminių spalvų san- tykį, gausime kitokią ketvirtą …
Excerpt
65 pav. Spalvų kūno mode- lis - dvigubas kūgis (Velič- kovskis ir bendraaut.,1973 ). V - violetinė, M - mėlyna, Ž-M - žaliai mėlyna, Ž - žalia, Ž-G - žaliai geltona, G - geltona, O - oranžinė, R —- raudona, Kiti paaiškinimai tekste. Joda giančią kūgių …
Excerpt
"A > - = T T 0 ž T 17 + . aff VŽ 01 82 03 04 05 86 87 08 X 66 pav. Spalvų trikampis (Vudsonas ir Konove- ris, 1968 j. TD - tipografinių dažų spalvų zonos ribos; C - citrinos spalva, P - pomidoro spalva, B - balta spalva, R - raudona, Oran. - oranžinė. …
Excerpt
apskritai, kūnų spalva priklauso nuo to, kokio ilgio bangas sugeria paviršius. Pavyzdžiui, mo- lLinis puodas mums atrodo raudonas todėl, kad molyje esantys dažai sugeria violetinius, mėly- nus ir Žalius spindulius. Mėlyni dažai sugeria ilgabangę (raudoną, …
Excerpt
vinius požymius? Kokie spalvų skyrimo mecha- nizmai? Žmogus skiria apie 200 spalvų tonų.Gal būt, tinklainėje yra 200 pigmentų rūšių, atitinkan= čių atskirus spalvų tonus. Tokia idėja iš karto atkrenta, nes Žmogus gali lavinti spalvinį regėji- mą ir …
Excerpt
įr disimiliacijos procesai. Pirmoji substancija yra geltonos -mėlynos spalvų suvokimo pagrindas, antroji - raudonos -žalios, trečioji - baltos-juo- dos. Šviesių (raudonos, geltonos, baltos ) spal- vų pojūčiai atsiranda vykstant disimiliacijos pro- cesams, …
Excerpt
miausia neurofiziologai ėmė ieškoti skirtingų pig- mentų ir kūgelių. Buvo nustatyti tokie faktai, 1, Kolorimetrijos (spalvų matavimo ) metodo esmė - monochromatinių spalvų lyginimas su spal= vų maišymo keliu gauta spalva, Ne visose spekt- ro dalyse šis …
Excerpt
rūšių kūgeliai, turintys skirtingus pigmentus.Vie - nų kūgelių jodopsinas geriausiai absorbuoja 445- 450 nm ilgio. šviesos bangą, antros rūšies kū- gelių - 525-535 nm, trečios - 550-570 nm. Šie šviesos absorbcijos maksimumai atitinka vėl mė- lyną, Žalią …
Excerpt
4 4001 Š 58- 3 D į S S = IU g P m 400 790 švresas bangos MRis, RM 69 pav. Tinklainės ganglijinių ląstelių ir regos nervo skaidulų reakcijų į monochromatinę šviesą tipai (Granitas, 1967). maciją apie raudoną, žalią ir mėlyną šviesas, De Valua (1965) …
Excerpt
sa sukėlė "on" atsakymą, o periferijos dirgini- mas - "off". Papildoma raudonai spalva - žalia sukeldavo visiškai priešingus atsakymus: cent- ro dirginimas - "off", periferijos - "on". Buvo neuronų, kurie "on" reakcija atsakydavo į re- ceptyvinio lauko …
Excerpt
Dar iki oponentinių neuronų suradimo kaikų- rie mokslininkai teigė, kad Žmogaus spalvinį regė- jimą iš dalies paaiškina tiek Heringo, tiek Jungo- Helmholco teorijos. Šių teotijų prieštaringumas yra tik tariamas. Trikomponentinė teorija gerai pa- aiškina …
Excerpt
"abejo, abiejų teorijų sujungimas dar nėra baigtas, ir tikrieji spalvinio FPegėjimo neurofiziologiniai me- chanizmai nėra visiškai aiškūs. Spalvoms jautrūs daugelis gyvūnų: ir stubu- riniai, ir bestuburiai. Trys pigmentai surasti auksinės žuvelės, staro, …
Excerpt
+1eponf so;5Zz0pnu (tp -Ną OUTUSsAK8S tUunyeUu SsorDUPIMSsIAI *'so4xeS Gizpsu softoNnijOAXZ > 7e10d0 (rerdurexį. į ) NITSSNA AI (rerduroyerzeįs) Nirogsųs SeįKpo1ed PiUuNnaKS NU -STAX9IŲ S9LL (T26T 'seA0110) efronijoAD3 ounfašas1 orutapedS "And 22 - …
Excerpt
Uftravio- etinė 73 pav. Žmogaus ir bitės spalvų ratai (Berto- nas; 1972). Bitės nemato raudonų, o Žmogus - ultravioletinių spindulių. suvienodina. Daltonįzmas - dažnokas spalvinio regėjimo sutrikimas. Jis būdingas maždaug 104 vyrų ir 0,59 moterų. …
Excerpt
teranopus (aklus Žaliai spalvai) ir tritanopus (aklus mėlynai ir violetinei spalvoms). Dažaiau- siai pasitaikantis regėjimo sutrikimas > jau minė= tas daltonizmas (protanopija). Protanopai mato tik dviejų tipų atspalvius: geltonus ir mėlynus. Raudonos ir …
Excerpt
pirhi spalvimo rEgĖ//MO Slikiai m ---- Ji L aa ----- £ $ 2 Kaamolnė MIMOCNO - Dre/vIYNa- įPrelvanazja Indžjja 22 TIT TI „---71M----Ą „----/ |M—----—-ą į X N 1 -—- + | Bafa- | |Deuter-| | ThT- Bd'a- | | Deuter-| | TH7- nd | | anona | |Oraorng- | | ja a ja …
Excerpt
jektai turi specifišką erdvinę išraišką. Suvokimo objektas arba fisūra visada ryškesnė už jį su- pantį foną. Tarp objekto ir fono visada yra tam tikra dinaminė pusiausvyra: tai, kas buvo suvo- kimo objektų, gali tapti fono dalimi, ir atvirkščiai. Vienas …
Excerpt
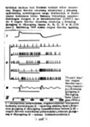
tyvinius laukus turi šoninio kelinio kūno neuro- nai. Regos žievės neuronų atsakymai į difuzinį apšvietimą sudėtingesni negu tinklainėje ir šoni= niame keliniame kūne. Vakarų Vokietijos psicho- fiziologas Jungas ir įo bendradarbiai (1957) ra- do 5 regos …
Excerpt
nereaguoja į dirginimą difuzine šviesa (A neuro- nai). B neuronai (254) jaudinimu reaguoja į švie- sos įjungimą ir slopinimų - į šviesos išjungimą. C neuronai reaguoja slopinimu ir į šviesos įjun- gimą, ir į išjungimą. D neuronai reaguoja priešin= gai B …
Excerpt
būdino Lindsėjus ir Normanas (1974): "... jis są- žiningai perduoda informaciją sekančiam perdir- bimo aukštui"!. Žinant šoninio kelinio kūno abi- pusius ryšius su retikuline formacija, regos Žie- ve ir kitomis smegenų struktūromis, jo "sąžinin- gumų" …
Excerpt
tinklainės projekcija kituose 17 lauko sluoksniuo- se. 18 ir 19 laukų ryšio taškas į tašką su tink- laine jau nėra. ' Formos detektoriai Susipažinę su šoninio ke- linio kūno neuronais, Hjubelis ir Vizelis (Hiubelis, 1960) ėmė mikroelektrodais "medžioti" …