Excerpt
- Patalpų pavadinimas inimalus ap- viestumas liųk - ais emputės kaitinimoliumines cencinė: £ — ie Projektavimo salės, mašinraščio biurai Mokyklų klasės, la- boratorijos ir moky- mo kabinetai Klasės lentos r Rūbų, avalynės, au- dinių, galanterijos, knygų …
Excerpt
Minimalus ap- Paviršius, Patalpų pavadinimas | šviestumas liuk- |Įkuriam ski- | sais riama ap- kaitinimolliumines įšviestumo 4 Iemputės| cencinėš norma lempos Gyvenamųjų butų 30 75 0,8 m nuo Įkambariai 4 grindų “ įKino teatrų salės 30 160 J «t 20-80 Ik, …
Excerpt
žvakės liepsnos - 5, Žibalinės lempos lHepsnos - 6-15, baito popieriaus (saulės šviesoje) - 11- 20, sniego (saulės šviesoje) - 30, 40 vatų elekt- ros lemputės - 2000, saulės (horizonte) - 3600, saulės (zenite) - 1650000. Slenkstinis šviesos ryškumas …
Excerpt
Šviesa į akį atkeliauja nuo įvairiausių kūnų. Vieni paviršiai patys spinduliuoja šviesą, kiti at- spindi beveik visą į juos krintančią šviesą, treti - tik dalį į juos krintančios šviesos, ketvirti yra kliūčių. Dauguma mus supančių objektų iš dalies …
Excerpt
sumaišius dvejopus, trejopus- ir tt. monochrometi - nius spindulius, Spalvą apibūdina trys pagrindiniai požymiai: ryškumas (šviesumas), spalvinis tonas ir sodru- mas. Praėjusiame paragrafe sužinojome, kad švie- sos ryškumas yra intensyvumo, …
Excerpt
S Gela/a/ žaliai: RD Ak g | GeINA mėlyną 1 BOUSUOT gelta ekvVai NUATO/NA T S „R Š a JA Valeniė sa 285 Aurpurinės 63 pav. Spalvų ratas ĮVelškovekis ir bendraaut, 2973). Paaiškinimai tekste. lima gauti maišant įvairiausius monochromatinius spindulius. Dvi …
Excerpt
ta, ir juoda (įvairios pilkos spalvos), Jeigu mi- šinyje yra didesnis procentas A spalvos, tai mi- šinio spalva bus tos pačios spalvos, kaip ir A, tik mažesnio sodrumo (dėl B priemaišų). Maži- nant B spalvos kiekį mišinyje, A spaivos sodru- mas didėja. …
Excerpt
organai, priešakinės galūnės ir t.t. Todėl negalima psichikos evoliu- cijos atskirti nuo psichikos ir elgsenos morfofiziologinių koreliatų. Koreliacinė zoopsichologija ir tiria priežastinius ryšius tarp psichi- nių ir morfofiziologinių požymių. Psichika …
Excerpt
lizuotą viso organizmo reakciją. Daug sudėtingesnė ir labiau cent- ralizuota dygiaodžių radialinė nervų sistema. Jūrų žvaigždės ner- vų sistemoje ne tik kur kas augiau neuronų, bet jie ir labiau specializuoti. Recepciniai, asociaciniai ir efektori iai …
Excerpt
o tuo pačiu ir elgsena pri- klauso ir nuo aplinkos, prie kurios gyvūnas yra prisitaikęs (N. Vasilevs- kis, 1979). Smegenų ontogenezė. Bręstant elgsenai ir psi- chikai, bręsta ir jų mate- rialus substratas — sme- genys. Neuruliacijos — nervų audinio …
Excerpt
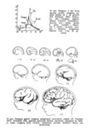
1 Karvelis 71 pav. Encelalizacija — stuburinių galvos smegenų progresyvus kitimas (D. Hju- 9) belis, 1 1800 L (2 NN --— 1400 J=—T— Bž m: NM 1000 --SDAN , ' = (5, Di 4 607 ; =—15 | 200 J! L —,- == 200 V 600 4 1000N I400M4 1800 > < 1 » M - 200 72 pav. …
Excerpt
Brarčuolys MilGrkOnArijos Aeurono 3ū 73 pav. Simpatinės nervų sistemos neurono aksono augimas (R. Levi-Montalcinis ir P. Kalisanos, 1979). Aksono galūnės kryptingą augimą lemia vadinamasis augimo faktorius (neurobiotaksis). /—4 — aksono augimo stadijos …
Excerpt
74 pav. Zmogaus ir kai kurių gyvūnų galvos smegenų ūu- gimo tempai iki ir po gimimo (Dž. Dobingas, 1967). Ordina- čių ašis — smegenų. augimo tempas (vienetai santykiniai); abscisių. ašis — laikas: žiurkė ir jūros kiaulytė — dienos; šuo ir kiaulė — …
Excerpt
o po gimimo — dėl neuronų ataugų ir pagalbinių elementų augimo bei brendimo. Aksonai auga ir sinapsės susidaro daugelį metų, o gal ir visą gyvenimą. | | | | Mažai tyrinėtas žmogaus bei gyvūnų elgsenos ir smegenų liloge- nezės bei ontogenezės ryšys. Dar …
Excerpt
Sia... 75 Gtotuų,.. ZiCUna PolisiaGps1nes L22 Tarpiniai neusnnai NAarrsiDAOS:NeS Sadidulas 5 5 Sensor: 01 iEUTONai 77 pav. Moliusko apiizijos žiaunos įtraukimo rejlekso modelis (E. Kendelas, 1979). Prisilietus prie sifono arba mantijos ataugos, aplizija …
Excerpt
roniniais, cheminiais ir kitokiais elementais. Analoginiai modeliai padeda imituoti kai kuriuos elgsenos aspektus, tačiau jie negali pakeisti realių elgsenos mechanizmų aiškinimo. Gilėjant žmogaus pažinimui, kuriamos koncepcijos vis geriau atitinka …
Excerpt
Cruze W. W. Maturation and learning in chicks.— J. Comp. Psychol., 1935, v. 19, N. 5, p. 371—409. Cuvier F. cit. pagal Fluransą P. (1900). Darelas Dž. Sugaukite man kolobusą.— V., 1978. Darvinas Č. Rūšių atsiradimas.— V., 1959. Dekartas R. Rinktiniai …
Excerpt
Hess E. H. Imprinting.— Sci., 1959, v. 130, N. 3376, p. 133—141. Hess W. Die Regulierung des Blutkreislaufes.— Leipzig, 1930. Hilgard E., Marguis D. Čonditioning and learning.— N. Y., 1940. Hubel D. H. The brain.— Sci. Amer., 1979, v. 241, N. 3, p. 38—48. …
Excerpt
Papez J. W. A proposed mechanism of emotion.— Arch. Neurol. and Psycjiat., 1937, v. 38, N. 4, p. 725—743. Pavlov I. P. Sur la sėcrėtion psychigue des glandes salivaires.— Arch. in/ernat. de physiol., 1904, v. 1, N. 1, p. 119—135. Pitagoras ĮLiudijimai].— …
Excerpt
Wo!fe J. B. (1936) cit. pagal Dembovskį J. (1963). Ycarkes R. M. Almost human.— N. Y., 1925. Yearkes R. M. Social behavior oi chimpanzees: dominance between mates, in relation to sexual status.—J. comp. Psychol., 1940, v. 30, N. 1, p. 147—186. Zubavičius …
Excerpt
Boūronuc H. IO. HekoTopmie AaHHBIe K BONpocy O reHeaHce HATenNeKTA.— B kR.: Peduekcbi, HHCTHHKTBI H HaBbikų. M., 1936. Boūronuc H. IO. IlpexmicTopua uuTen1eKTa — M.—/I., 1949. Bonoxoe A. A. OnToreneTHųecKaa 3BONNONHA YCIOBHOPeNEKTOPHOK XEATEJNBHO- cTH.— B …
Excerpt
Kpyuunckui JI. B. OopMupoBanne nNnoBexeKHHA > XHBOTHBIX B HOPME I NaToJNOrHH.— „1960. Kpywunckui JI. B. BuonoruueckKe OCHOBbI! paccyAOWKHOoR AEATENbHOCTH. DBONIOUNHOH- HBId It dH3HONOrOoreHeTHYeCKHA aCNeKTB! NOBexeHHA.— M., 7. Kpywuunckui JI. B. …
Excerpt
Il naTon. 3ako0Hbi M nocAeCJOBINE K 3ak0HaM.— B ku.: IlnaTon. MonHoe c06p. TBOpe- HK. I6., 1923, T. Il naTOR. Teder MJ, 1936. Ilose0enue mneKOnKTaIHxX.— M., 1977. Ilonakos F. H. Mpo6newa rMponcxoKAeKHIA peĖ-1CKTOPHBIX MEXaHII3MOB M., 1964. ITonyzae6a A. …
Excerpt
Yxromnckud A. A. HucruuKT H AOMHHaKHTa.— B kH.: YxrowMcKud A. A. Co6p. cox., 1950, T. I, c. 186. da6p K. B. HucrnKkT W HpaBhi HacekoMBIx.— CI6., 1905—1908, T. 1—2. da6p JX.-A. )Kua3ub naceKOoMbix. Paccka3bt sHToMONOra.— M., 1963. ba6pu K. 3. OcuoBbi …
Excerpt
DALYKINĖ RODYKLĖ Abiausis girdėjimas 74 Adaptacinė radiacija 20 Aferentinė sintezė 49 Agresija 93, 146—147 Aklimacija 112 Aklimatizacija 112 — ir elgsena 112—114 Aktyvumas, ritmika 86 — koeficientas 88 — bendrasis 104 — specifinis 104 Alkis 121 Altruizmas …
Excerpt
Fechnerio dėsnis 67 Feromonai 75, 139, 160 — pavojaus 161 Filogenezė 167 Fobijos 179 Fotokinezė 38, 39 Fototaksis 37, 38, 177 Frustracija 95 Funkcinė sistema 6, 66 Fuzija 71 Gameta 125 Gąsdinimas 109 Genas 167, 168, 174, 176, 199 Generalizacija 50, 53. 65 …
Excerpt
Omatidijos 72 Ontonegenezė 167 — elgsenos formų 183, 184 — intelekto 185 — išmokimo 184 — sensomotori ių funkcijų 182, 183 Otolitai 80 Partenogenezė 125 Paveldėjimas 6, 169 Peštynės 144, 147 Pyktis 146 Poikilotermija 77 Pojūtis 193 Poliginija 141 …
Excerpt
Seima 130, 131, 136 — bičių 137—140 — monogaminė 130, 132, 136 — motininė 130 — poligaminė 130, 132, 136 — polimorfinė 135 — skruzdžių 140, 141 — termitų 141, 142 — tėvinė 130 Šlapinimasis 124 Šlykštumo skalės 91 Šoki i 157 Šoninė linija 72 Švytėjimas 100 …
Excerpt
Hidra 99, 100, 197 Koraliniai polipai 198 Medūza 197, 198 Tipas. Plokščiosios kimnėlės (Plathel- minthes) — 69, 88, 125, 194, 198 Planarijos 37, 77 Tipas. Žieduotosios kirmėlės (Anne- lida) — 88, 198 Acholoe 100 Odontosyllis 100 Sliekai 88, 125 Tipas. …
Excerpt
Tipas. Dygiaodžiai (Echinodermata) — 19 Jūrų žvaigždės 125, 198 Ophioderma 136 Tipas. Chordiniai (Chordata) — (stuburi iai) 64, 71. 203 Klasė. Apskritažiomeniai (Cyclosto- mata) — 77 Nėgės gėlavandenės 80 — jūros 80 Antklasis. Žuvys (Pisces) — 4, 16, 24, …