Excerpt
7 lentelė, Apibendrintas Merkelio, Veberio- Fechnerio ir Plato-Stivenso dėsnių formulavimas (Keidelis, 1975) Dėsnis Autorius Diferencinė Integralinė forma forma IMerkelis AS=ktAi Ss = k'(I-Ig) Veberis AS =k AL 1 I I EFechneris S=k1n — Plato AS = —L 1n S …
Excerpt
ir verbalinę. Pagal tai Pavlovas išskyrė ir dvi signalines sistemas: Į-ją ir Il-ją. Pirmąją signa- linę sistemą turi ir gyvūnai, ir Žmogus. Bet koks stimulas, derinamas su reikšmingu biolosiniu dir- gikliu (maistu, sužeidimu ir kt.) tampa to dirgiklio …
Excerpt
jos išeina, mums prieinama. Kibernetika pasinau- dojo ortodoksaliojo biheviorizmo schema. Šioje schemoje S yra stimulas, R -—- reakcija. Bihevio- ristų Nuomone, galima apsiriboti šių dviejų konti- nuumų santykių analize;- Psichofizikinis tyrimų as- pektas …
Excerpt
cijos kiekio vienetu yra bitas (dvejetainis viene- tas), kuris sutrumpintai rašomas dv. vnt. Vienas dv. vnt. (bitas) - informacijos kiekis, kurį gau- na Žmogus, teisingai parinkęs vieną iš dviejų vie - nodai galimų įvykių. Teisingas tono iš 2 tonų "abė- …
Excerpt
8 Ientelė. Informacijos kiekis, kurį gal gus priimti vienmačiais stimulais (Lomova Stimulo po- |Perduota informa - Modalu- |žymis, kurio įcijos, dv. vn ė mas gradacijos |Trumpa įHgaeks- buvo iden- |ekspozi-|pozicija titikuojamos įciją VizualiniaiRodyklės …
Excerpt
65 Stimulo po- |Perduota informa - Modalu-| Žymis, kurio [cijos, dv. vnt. Autorius mas gradacijos [Trumpa Į[Ilga eks- buvo iden- Įekspozi-|pozicija tifikuojamos [cija | Geometri-- |2,0-2,2 Erikse - nių figūrų as ir plotas Heikas (1954) 2,6 2,7 Polakas ir …
Excerpt
as Modalu - Stimulo po- žymis, kurio Igradacijos buvo iden- tifikuojamos Įcija Naktiliniai» WVibrac ijos. in+ braciniaitensyvumas | Vibracijos trukmė Vibracijos įlokalizacija Perduota informa- cijos, dv. Autorius Trumpa Tga eks- kspozi-Ipozicija Dželdar- …
Excerpt
Informacijos perdavimui svarbus veiksnys - laikas. Kuo trumpesnis stimulų pateikimo laikas, tuo Žmogus sunkiau juos identifikuoja. Iš 8 len- telės matome, kad trumpos ekspozicijos metu per- duodamos informacijos kiekis 0,1-0,7 bito mažes- nis, negu ilgos …
Excerpt
jamų) tonų. 9 lentelėje pateikti įvairių stimuių santykinio ir absoliuiaus skyrimo duomenys. Pavyzdžiui, Žmogus lygindamas vieną su ki- tu, skiria 128 spalvų tonus. Absoliučiai vertin- damas (identifikuodamas ž žmogus skiria tik 12- 13 atspalvių. Panaši …
Excerpt
Stimulia- įDažnumo di zonas |Dažnumo įmas cijos rū- |Minima-| Maksimalus, Santyki- |Absolių » is lus nis tus Baltas 1 per- |2000 per- |460per- |Nežino- triukšmas | trūkis [trūkių per įtrūkių mas sų ritmiš— 1 s (vidu-Įdažnumo kais per- tinio stip- …
Excerpt
mos kanalėlių skaičius. Todėl toks perdavimas laike ribotas, Lygiagretus informacijos apdoroji- mas pavaizduotas 15 pav. "| Zėjimas „Informacijos, perdirbimas g „Zi - ps Į Viauztinis | „de | | Gesčas 1 | | | Irbi- 1 "nas Ir spren- M Kustinis | ug N AAS Į …
Excerpt
4, OBJEKTVYYVUS SENSORINIŲ SISTEMŲ TYRIMAS Subjektyvūs ir objektyvūs metodai. Psichiniai reiškiniai nėra ore skraidančios "idėjos", "sielos" arba "dvasios". Jie yra smegenų funkcija ir eg- zistuoja tik tiek, kiek egzistuoja pačios smege > nys. Pojūčiai, …
Excerpt
atitinkamais psichinės veiklos rodikliais. Kuo di- desnis koreliacijos (ryšio) laipsnis tarp konkre - čių psichinių ir fiziologinių reiškinių, tuo .-patiki- miau subjektyvius atsakymus galima pavaduoti tiziologiniais rodikliais. Fiziologinio lygio …
Excerpt
ti Šios grandies vietą bendroje veikloje padeda vėl interpretacijos metodas, Tokiai fiziologinių fak- " tų interpretacijai reikalingos psichologiniais meto- dais gautos žinios, Jeigu fiziologas nieko nežino- tų apie elgesio aktus, reakcijas, pojūčius, …
Excerpt
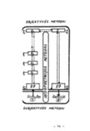
OBJEKTYVŪS METODAI A — A m Rapžas - ODAS EE Rf "ED | Rdkija (R) | SUBJEKTYVŪS METODAI II T ao 0 i T Š || (8) INTERPRETACIJOS -MET - 74 …
Excerpt
":- am SP RP ED END SDD SD LEP GP SEN KZ A 7 PE „Ayektyviai“ PP SD P DD GD GRD SD DD D O SAP LED AP OO Opa „ Suoatiyviai “ ;- —4 ) L 17 pav. Subjektyvaus ir objektyvaus sensorinių sistemų tyrimų schemos (Keidelis, 1975). Elektrofiziologiniame tyrime …
Excerpt
ir gyvūnų sensorinę veiklą Šaltinis yra objekty- vus tyrimas. Tokiame tyrime Žodžius "juntu", "ma - tau"; "skiriu" ir tt pakeičia įvairūs elektrofizio- loginiai rodikliai. Kadangi fiziologiniai (objektyvūs ) metodai tai- komi psichologinių faktų …
Excerpt
į kaimyninius taškus. Pradiniuose evoliucijos eta-, puose jaudinimas sklinda visomis organizmo kryp- timis. Vėliau jaudinimas darosi vis iokališkesnis, o jo sklidimas vis kryptingesnis. Yra poveikių, kurie dėl tam tikrų fizinių-cheminių pakitimų didi- na …
Excerpt
(a) GAUTI „nseu seuniapni 's( ASP sąpaįstt SiON7 smotdisd "(V sguntaPni sof(s0ZNJUT BXUIvns (€) stuojJt? ns (2) RumIIOLOUI srauni so1l -nu(T) SAUMAB snaotdasd „sežundiii 94A TTYP sepaįsti UBI dxe) SASAU «go(Įo UNI seBUN4I1S exMA sAĮYP sa[218*1 so»NSIV …
Excerpt
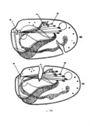
19 pav. Nervinių ląstelių (neuronų) įvairovė (Poliakovas, 1964 ), 1 - amakrinė tinklainės ląstelė; 2 - uodimo svo- gūno neuronas; 3 - spinalinio ganglijo neuronas; 4 —- stuburo smegenų motoneuronas; 5 - apati- nis alyvos neuronas; 6 - viršutinio dvikalnio …
Excerpt
daro dešimtis ir šimtus kontaktų- su kitais nervi- niais eiementais arba raumenų ląstelėmis. Pagrindinė neuronų bendravimo priemonė yra nerviniai impulsai. Nervinis impulsas - tai atsi- radęs somoje ir sklindantis aksonu fizinis-che- minis procesas. …
Excerpt
———— AMEE J | 4 == p- PAMESTA | — p A Ask Lai ab -—-——— Lt+5+-R-—---—-— į T —“uO SN G S AEPNMAYZAC/JA +! + + : ki“ +1 k +] I Į I Į ! 1 z l | Į …
Excerpt
„erepou?109 „erundeuis1s09 ((onuvuidoT“ - gasdSs reraious10d „erundeU!s 1504 tonueuonai „ asai „suomauU susi XI sureusti! ausų?“ ownAB3 +eratIIU s10d „erundevis at srauosA? monzuorot 9 at monzrusis!W saurpriAi? saunpvaiS?“ (orsiou—o“ oundi a) osmdut oruaU …
Excerpt
neigiamesnis išorės atžvilgiu ir tolsta nuo slenkš - tinės depoliarizacijos. Kuo daugiau atitoliname ramybės potencialą nuo sienkstinės depoliariza - cijos reikšmės, ty. kuo daugiau hiperpoliarizuo- jame neuroną, tuo labiau padidėja nervinio impul- so …
Excerpt
Atkeliavęs į sinaptinę galūnėlę, nervinis impul- sas dėl didelės membranų varžos negali "peršokti" į kitą nervinį elementą. Todėl čia jis ir užgęsta. Tačiau jam veikiant iš sinaptinės gailūnėlės iš- siskiria medžiaga, vadinama mediatoriumį, kuri keliauja …
Excerpt
nervų sistema. Nervų sistemos evoliucijoje išryš - kėja keletas tarpusavyje susijusių tendencijų; se- gregacija - nervinių elementų su panašiomis funkcijomis jungimasis į grupes; centralizacija - grupių jungimasis į centrinį organą - centrinę nervų …
Excerpt
jasi į grupes - mazgus arba ganglijus (21 pav. ). Pradinėse stadijose atskirų mazgelių dominavimo dar nėra: kiekvienas kūno segmentas su savo mazgelių pora išlieka daugiau ar mažiau autono- mišku vienetu. Jau nariuotakojų (vabzdžių, vėžia- gyvių) ir …
Excerpt
ss KUSB3US sorsoSfad - KM Isąpgus8dWS — „ įs4uošous sgumMPiA = A. įs4uo89US sau -rda6į - IN ts ZUusB UIS sgurrv8 — 1 ISAIPIS sorS —owerzpon - 1 ( snueSouz 'OpSNIJI 'oz SP "On AA ĮoUoyUTINS ) sAusBau:s soAT9S8 hunaXB Nrutvaną ns - 8-6 swvusįsįs MMAADU …