Excerpt
Adaplacija silpnam ATI Taaptaci/a stipriam dirginimai JavtrumaslE= WJ „ Laikas „min. 42 pav. Sensorinės adaptacijos silpnam ir stip- riam dirginimams kreivės. biausia skirtumų priežastis ta, kad skirtingi ana- lLizatoriai adaptuojasi nevienodai Greitai ir …
Excerpt
pradeda keliauti nerviniai impulsai. Pradžioje jų dažnumas labai didelis, tačiau laipsniškai jis ima mažėti (40 pav., D). Sensorinės adaptacijos mechanizmai sudėtin- gi. Granito (1957) nuomone, pagrindinė adapia- cijos priežastis yra aferentinių galūnėlių …
Excerpt
1 3 L š 2 š 4 6 43 pav. Įvairių receptorių adaptacijos pastoviam dirginimui kreivės (Edrianas, 1928 J. Kuo kreivė arčiau nulinės tHinijos, tuo Žemesnis receptoriaus aktyvumas, I - varlės raumens receptorius; IN - katės spau- dimo receptorius; II - …
Excerpt
Žžinimas arba padidinimas, pertrauka, pašalinis sti- mulas ). Sensibiliegacija ir inaktyvacija,. Sensorinė adap- tacija, pripratimas ir nuovargis atsiranda dėl! ilga-> laikės stimuliacijos. Tačiau sensorines tunkcijas ilgesniam ar trumpesniam laikui gali …
Excerpt
Analizatoriaus žievės atskirų taškų jautrumą ga Lima keisti atitinkama Žodine instrukcija, nusista- tymu ir kt. (Čiuprikova, 1968). Sensorinės siste- mos įautrumas priklauso nuo amžiaus, endokrini- nių ir kitų vidaus terpės veiksnių. Pavyždžiui, iki 25-30 …
Excerpt
ruota akis - tik 0,1 mm tarpelį, Audinių dažyto- jai skiria apie 60 juodos spalvos niuansų. Labai tobula sūrio, vyno, tabako ir arbatos degustato- rių uoslė ir skonis, dailininkų sugebėjimas skirti formas, proporcijas ir spalvos tonus. Kravkovo (1946) …
Excerpt
t skyrius. REGOS SISTEMA v 1. ŠVIESA IR AKIES OPTIKA Regos funkcijos. Vieni mokslininkai mano, kad regos organu Žmogus gauna 804 visos in- formacijos, kiti šį skaičių padidina iki 904, Ta- Čiau tiksliai regos kanalu gaunamos ifKHormaci- jos 'dar niekas …
Excerpt
gos dirgiklis. Žodis "energija" reiškia, kad švie - sa gali atlikti tam tikrą darbą: šildyti kūnus, su- kelti chemines reakcijas ir Lt. Šviesos srautas sudarytas iš mažiausių dalelyčių - fotonų (arba kvantų J. Ore šviesos dalelytės juda 300000 ki- lometrų …
Excerpt
Perca ŠA, Dar Niutonas įrodė, kad baltos šviesos srau- tas nera vienalytis. Jis sudarytas iš Įvalraus I!- Bio elektromasnetinių bangų. Specialios prizmės mų TTT | InArarav | Jigos radijo | donizji | dangos „i [mezk=B) Ni | 7umpos | "—— ji Į radijo dangos …
Excerpt
pagalba Niutonui pavyko suskaidyti baltą šviesą į atskiras monochromatines šviesas, Fizikinis monochromatinės šviesos rodiklis yra bangos il- gis, psichologinis - atitinkama spalva. Monochro- matinės šviesos pagal bangos ilgį išsidėsto taip: violetinė - …
Excerpt
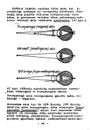
Akies sandara. Periferinę regos sistemos da- l sudaro akių obuoliai, juos judinantys raume- nys ir apsauginiai duriniai (vokai sų konjunktyva ir ašarų liauka). Akis dažnai lyginama su foto- aparatu. Ir vienas, ir kitas turi optinę sisterną, pritaikymus …
Excerpt
45 pav. Akis ir foto - aparatas (Uoldas, 1974), Ir akyje, ir totoapa - A IBP < ) rate yra lęšiai, foku- A sirai T, suojantys apverstą atvaizdą šviesai jautriame sluoksnyje. Fotoapara - to diafragmą atitinka akies rainelė. 1 > konjunktyva; 2 - lęšiuko …
Excerpt
Vidinis gyslainės paviršius padengtas pigmen- tuotų ląstelių sluoksniu, Vidinis piementinio sluoks- nio paviršius ribojasi su trečiu akies apvalkalė- liu — tinklaine (retina). Šiame apvalkalėlyje yra išsidėstę šviesai jautrūs elementai - fotorecepto- …
Excerpt
mo ir Kkonvergentinius -divergentinius judesius, Abiejų akies obuolių sakadiniai judesiai sinchro- niški, Jie gali būti valingi ir nevalingi. Sakadi- nių judesių amplitudė svyruoja nuo kelių kampi- nių minučių iki keleto laipsnių. Konvergentiniai- …
Excerpt
da skirtingu greičiu. Dėl šios savybės šviesos spinduliai, pereidami iš vienas terpės į kitą, lūžta. Lūžimno kampas priklauso ne tik nuo me- džiagos tankio, bet ir nuo besiliečiančių terpių paviršiaus kreivumo. Prieš pasiekdami tinklainą, šviesos …
Excerpt
Ryškiam vaizdui tinklainėje gauti būtina, kad šviesos spinduliai, praėję optinę akies sistemą, susirinktų tinklainėje. Gamta "suderino" akies laužiamąją galią ir jos ilgį (atstumą nuo lęšio iki tinklainės ). Kam teko fotografuoti, Žino, jog, keičiantis …
Excerpt
46 pav. Akomodacijos reiškinys: lęšiukas iš- gaubtas, Žiūrint į arti- mus daiktus, plokščias, žiūrint į tolimus daiktus. | žiamųjų galių), 20-ties metų jaunuolio akių ako- modacijos diapzonas sumažėja iki 11+ 1,5 D, 50 metų - 241 D, 30 metų - 84+2D, 40 …
Excerpt
mą praėję spinduliai nesusirenka viename taške. Dėl to projekcija yra neryški, Antra, regėjimo ašis, t.y. tiesioji, jungianti matymo tašką ir cent- rinę duobutę, nesutampa su akies optine ašimi, Jos susikerta sudarydamos 59 kampą. Dėl to šviesos …
Excerpt
Ryškus objekto vaizdas būna tada, kai jo projekcija sutampa su receptorių sluoksniu. Nor- malių akių įvairūs trūkumai kompensuoja vieni kitus, ir gaunamas vaizdas būna pakankamo ryš- kumo. Normali akis vadinama emetropine (47 pav. ). 2 47 pav. Lūžusių …
Excerpt
to gavo ištisą diapazoną subjektyviai įvertintų in- tervalų. Absoliutus intervalų dydis buvo nevieno- das, tačiau šis nevienodumas pasirodė besąs dės- ningas. Kiekvienas intervalas buvo lygus prieš jį einančiam intervalui, pakeltam tam tikrų laipsniu, …
Excerpt
Ue92,) 2 as (sgl Sudrekiijaus Palensspavooo a + L a o H T 0 + 2 53 3 d 0 DirglhlAo PAREIGOS Į SELGGIDAa! vė.) 12 pav. Psichofizikinės elektrinio dirginimo, li= nijos ilgio vertinimo ir šviesos ryškumo suvoki- mo skalės (Veličkovskis ir bendraaut, 1973), …
Excerpt
kių ir intervalų tarp jų skalės. Atskaitos pradžia tokioje skalėje nėra fiksuota. Ją eksperimentato- rius parenka savo nuožiūra, Pavyzdžiui, tiriama - jam pateikiamas stimulas, sukeliantis atitinkamo dydžio pojūtį Po to eksperimentatorius paprašo, kad …
Excerpt
vadinimo (nominalo, vardo) funkciją. Tokių ska- lių pavyzdžiais gali būti klasikinių pokalbių kie- kybinės analizės rezultatai, įvairios objektų kla- sifikacijos, radijo detalių (pavyzdžiui, varžų) skirstymas pagal nominalus ir tt. Vieną ir tą pa- tį …
Excerpt
intervalais), vos pastebimų skirtumų nustatymas visam dažnumo ar intensyvumo diapazonui ir kt. Intervelų skalėse atskaitos pradžia parenkama laisvai. Todėl šios skalės nieko nesako apie nulinį (absoliutų) atskaitos tašką. Pavyzdžiui, Celsijaus …
Excerpt
tervalų (intervalų, atrodančių lygiais) metodas; 2) tiesioginio skaitmeninio įvertinimo metodas; 3) porinio lyginimo metodas; 4) rangų metodas; Su šių metodų aprašymu galima susipažinti Vud- vorsto ir ŠHiosbergo (1974) darbe, Stivensas (1974) percepcinius …
Excerpt
rio kontinuumui - vegais ir tt, Pateikęs standar- tinį stimulą, eksperimentatorius paprašo tiriamąjį parinkti iš serijos kitų stimulų dvigubai silpnes- nį arba dvigubai stipresnį už standartinį Galima paprašyti, kad tiriamasis parinktų trigubai, ketur- …
Excerpt
5 lentelė. Harperio ir Stivenso (1941) bandymo duomenys Standar - Svoris, įver- tinis (3 5 tintas kaip svoris, Svoriai lyginimui, g |"dvigubai leng- g | vesnis" (12 tiriamųjų vi- | durkis i £ 20 12, 14, 15, 16, 17, 18 15,8 40 24, 26, 28, 30, 32, 34 28,0 …
Excerpt
> — — o O GR 20 00 BD 0 0 Tandartinis suVis, gramai 8 13 pav, Subjektyvi svorio vertinimo skalė (Makarovas, 1959), A - priklausomybės tarp standartinio svorio, įvertinto kaip ————7—7 0,5 standartinio, gra- 0 LD 20 1020 do m fikas. B > svorio įver- SOrYs , …
Excerpt
6 lentelė. Subjektyvių < mės ir vieneto pavadinimas vensas, 1 Modalu- [Laipsnią Vieneto mas ir Įrodiklis | pavadi- kokybė nimas | Garsumasį 0,60 Sonas " 0,54 Suvokia- | 0,33 | Brilis mas ryš-- kumas M "0,50 Šviesu- 1,20 mas Kvapas 0,55 “ 0,60 Skonis 0,80 …
Excerpt
Modalu-; mas ir kokybė aipsnio rodiklis Vieneto pavadir nimas | | Sąlygos Autofo- ninė rea- kcija (re 4 akcija į savo bal- są Elektros srovė Suvokia Imas at- stumas mas il- gis Suvokia - mas plo- tas Objektų kiekis Garsų plakimas Suvokia-| 1,10 3,50 0,67 …