Excerpt
LTSR AUKŠTOJO IR SPECIALIOJO VIDURINIO MOKSLO MINISTERIJA VILNIAUS DARBO RAUDONOSIOS VĖLIAVOS ORDINO V. KAPSUKO UNIVERSITETAS A. BAGDONAS SENSORINĖS SISTEMOS II dalis ( Metodinė medžiaga ) Vilnius - …
Excerpt
I skyrius. BENDRI SENSORINIŲ SISTEMŲ ORGANIZACIJOS IR VEIKLOS BRUOŽAI (Tęsinys ) 5. TRANSFORMACIJOS IR KODAVIMO PROCESAI Specifinių enereijų dėsnis, Žmogus ir aukštes- nieji gyvūnai turi daug specializuotų sensorinių sistemų. Vienose analizuojamas garsas, …
Excerpt
Negalima teigti, kad specializuoti receptoriai visiškai nejautrūs neadekvačiamn dirginimui. Ne vienam pasipylė "kibirkštys" iš akių ir "suzvim- bė" ausyse smarkiai sutrenkus į kietą daiktą galvą. Tokių pojūčių atsiradimui reikėjo labai stipraus …
Excerpt
4, Neaiškų, kur lokalizuotos specifinės ener- gijos - pačiuose jutimo organuose ar galvos ir stuburo smegenyse. Aišku tik, kad nervų dalys smegenyse sugeba justi organus nepriklausomai nuo nervinių takų. Perirazavę Miulerio teiginius, gauname, kad vieno …
Excerpt
Jutimo organų specifiškumas - neginčijamas faktas. Specifiškumo idėją įtikinamai patvirtino morfologiniai ir elektrofiziologiniai sensorinių sis - temų tyrimai. Dirginant odą, atsiranda daug po- jūčių: šilumos, lytėjimo, skausmo ir spaudimo, At- rodytų, …
Excerpt
viklis, kuris transformuoja ir Kkoduoja signalus; ryšiai tarp receptoriaus ir smegenų centrų (ju- timo nervas) - tai ryšio kanalas, kuriuo keliau- ja užkoduota informacija. Smegenų centruose pra- sideda dekodavinmas. Kiekvienas sensorinis ner- vas ir …
Excerpt
Pojūtis |Receptorius Kritimo, |Vestibiulinio tiesiaei-.|aparato mai- gio ju- |šelių recep- dėjimo toriai Skonio Burnos ir liežuvio sko — nio recepto- riai Uodimo |Nosies vir- šutinės ert- mės gleivi- nio epitelio receptoriai Lytėjimo |Odos taktili — niai …
Excerpt
Adekvati energija Pojūtis |Receptorius Pozos irįRaumenų, Raumenų tem- Vidaus judėjimo |Įsausgyslių į pimas, susitrau+ (kines- |ir sąnarių kimas, galūnės teziniai )|mechano- | sulenkimas receptoriai | Į|(proprio- ceptoriai | echa- [Specialių Spaudimo stip- …
Excerpt
vadinami klasikiniais takais. Tačiau smegenyse: yra daug centrų, branduolių ir Žievės zonų, nie- ko bendro neturinčių su tiesioginėmis sensorinė- mis funkcijomis. Tokie centrai reguliuoja medžia- gų apykaitą, budrumą, kvėpavimą, širdies ir kitų vidaus …
Excerpt
AZ Turai! M — > ——-- ———- 36 pav. Specifinių ir nespecitinių ryšių schema. Retikulinė formacija yra sensorinių sistemų 8ą- veikos morfologinis pagrindas. Schemoje pavaiz- duotos tik klausos ir regos sistemos. Analogiš - kus ryšius turi ir kitos sensorinės …
Excerpt
Nežiūrint sensorinių ryšių konvergentinio-di- vergentinio pobūdžio, kanalinis analizatoriaus sandaros principas egzistuoja. Kanalinę senso- rinės sistemos sandarą gerai iliustruoja recep- tyviniai laukai. Pagal Edrijano (1928) apibrėži- mą, skirtą varlės …
Excerpt
37 pav. Varlės odos recep- tyviniai laukai. receptyvinių laukų morfolo- ginė schema. Skrituliukais pavaizduoti odos recepto- riai. B - odos receptyvinių Jaukų persidengimas, baigė, o sensorinio neurono reakcijos dingo, Tai- Bi funkcinio receptyvinio lauko …
Excerpt
yra neuronų, turinčių labai specializuotus -recep- tyvinius: laukus. Tokie neuronai vadinami detek- toriais. Regos sistemoje rašti spalvos, kampo, krypties įr padėties detektoriaii Klausos siste- moje --dažnumo ir moduliuotų garsų detektoriai, …
Excerpt
švietus šią omatidiją šviesos taškelių. Apšvietus kaimynines omatidijas, ekscentrinės ląstelės ak- tyvumas mažėja. Slopinantis kaimyninių ląstelių poveikis ir kuvo pavadintas šoniniu slopinimu. Slopinimas būna tuo stipresnis: 1) kuo stipriau dirginamos …
Excerpt
38 pav. Tinklainės ganglijinių ląstelių atsakymų į šviesos įjungimą ir išjungi- mą tipai, T. Šuje T | Paaiškinimai teks - te. ir suvbkimus. Jie yra aplinkos poveikių ir jų sa- vybių atspindžiai Okjektyvus pojūčio koreliatas yra nervinės veiklos pokyčiai. …
Excerpt
regos, skonio ir tt. (Hjinskis, 1971). Receptorius, kaip ir visos gyvos ląstelės, yra jaudrus,. Jo vi- dus užkrautas neigiamai išorės terpės atžvilgiu. Mechaninis arba cheminis receptoriaus membra- nos dirginimas sukelia depoliarizaciją, Ly. membra- ninio …
Excerpt
a) pirminiame receptoriuje: Recepcinis Mediatoriaus Stimulas., | potencialas | Nervinis išskyrimas (generacinis impulsas ir Lt potencialas į Transformacija enera- Mediacija cija b) antriniame receptoriuje: Recep-;Mediato-1Genera-| Nervi-|Media - , cinis …
Excerpt
Pecgptorius Šensoriniai nevronai “. Stirnvtas S L žugė Km €—————4 €-——————- campliugė pią mpulsų abžnymas NL : “Nervinių i | Aetepeinia patencialo Simulo stijanunas "Laikas Laikas Lai kas 39 pav. Stimulo energijos ir nervinių procesų stiprumo …
Excerpt
šiui su kūnu. Todėl Fechneris teigė, kad tiesio - ginis proporcingumas yra tarp stimulo ir jaudi- nimo, o logaritminis tarp jaudinimo ir pojūčio. Tuomet pagrindinis psichotizikos dėsnis turi bū- t užrašytas taip; S = klg E. Tokiam požiūriui ap- "Einti …
Excerpt
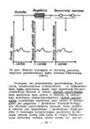
Du “o a PUlsėi /5ek. Impulsai /sek. LH Recepcinis palzme. TA V Ip . Recepeinis patare, i 2 40 pav. Ryšys tarp stimulo intensyvumo ir jau- dinimo procesų. Iš grafikų nesunku suvokti, kad logaritmavimas vyksta išorinės energijos transformacijos į ner- vinį …
Excerpt
spalvą, formą, dydį; cheminės medžiagos - pagal atomų išsidėstymą molekulėse ir tt Subjektyvių skyrimo laiptelių yra labai daug. Nemažiau turi būti ir nervinio proceso gradacijų. Kitas svarbus požymis - intensyvumas, kuris lemia pojūčio stip- rumą. Iš …
Excerpt
skaidulos, įnervinančios galūnių pirštus, pačios l- siausios. Jos turi apie 800 sąsmaukų. Kiekvieno- jo sąsmaukoje nervinis impulsas atgaminamas toks, koks jis buvo kitose sąsmaukose,. Jeigu ge- neracijos pastovumo nebūtų, nervinio impulso amp- NHtudė …
Excerpt
regos nervo skaidulų. Čia turėtų būti perduoda- mą 1000000bitų informacijos. Tačiau psichotizi- kiniame lygyje Žmogu: sugeba priimti ir perduo- u tik 4 bitus informacijos. Sensoriniu kodavimu ypač susidomėta, kai Edrijanas (1928) aptiko, jog nervinių …
Excerpt
s7—M—| iii) s“z=——M-į Ps+------11-+ | v. Sensorinio kodavimo nerviniais impulsais būdai. rodavimas kanalo numerių; B - sužadintų 1lų kiekių; C - impulsacijos trukme; D - la- Uu periodų; E - nervinių impulsų dažnumų; mervinių impulsų grupavimu ir …
Excerpt
procesą vis daugiau įsijungia receptorių ir ki- tų sensorinių elementų. Maksimalus dirginimas sujaudina visus sensorinės sistemos elementus. Šiam kodavimo būdui artimi kiti du būdai - tai kodavimas nervinių impulsų dažnumų ir kodavi- mas nervinių impulsų …
Excerpt
(41 pav., F). Ar tikrai sensorinėse sistemose koduojama tokiu būdu;kol kas nenustatyta. Nerviniai impulsai sal būti generuojami po vieną ir grupėmis arba, kaip kalba specialistai, sinchronizuotai ir desinchronizuotai (41 pav., H), Pavyzdžiui, miegančių …
Excerpt
ir jo priežastis. Kryptingą funkcijų kitimą galima užregistruoti tik stebint sensorinės sistemos veik - l4ą ilgesnį laiką. Stebint trumpai, kryptingĘ. kitimą užgožia atsitiktinės sensorinės funkcijos fluktua- cijos. Kad atsitiktinių fluktuacijų aibėje …
Excerpt
mo kitimas. Silpno dirginimo fone sensorinių sis - temų jautrumas didėja (slenksčiai mažėja), stip- raus dirginimo fone - mažėja (slenksčiai didė- ja). Šį teiginį galima pailiustruoti kasdieninio gy- venimo pavyzdžiais. Įeikinė vakare iš lauko į stipriai …