Excerpt
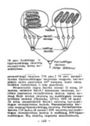
jaudina detektorių per slopinimo zoną, o šviesa - per jaudinimo zoną. Linijos, plyšio ir ribos de- tektorių reakcijos ir rsceptyvinių laukų formos pavaizduotos 76 pav. Iš paveiksliuko matyti, kad paprastų neuronų reakcijos dydis priklauso nuo stimulo …
Excerpt
Linijos defeklorius 8 Ply šio detektorius INIA= YS|e= Bi6os aetettorius di N Ė M m ——— —-—-— > > ———---- 76 pav. Katės regos žievės paprastų neuronų (linijos, plyšio ir ribos detektorių ) receptyviniai laukai ir reakcijos, A - atitinkamo stimulo …
Excerpt
6 ŠKK ?77 pav. Paprasto re- ceptyvinio lauko susi- darymas iš koncentri- nių receptyvinių laukų, kampu. Nesunku suvokti, kad sudėtingų neuronų receptyviniai laukai susidaro konverguojant neuro- nams su paprastais receptyviniais laukais. Tai ir įgalina …
Excerpt
78 pav. "Sudėtingų ir hipersudėtingų neuronų „receptyvinių laukų su- y KHipersudėlingas PEUVONAS sidarymas, (kampo detektorius) persudėtingo : neurono (78 pav. ) 78 pav. pavaiz- duotas hipersudėtingas neuronas reaguos, kaire-> gėjimo lauke pasirodys 459 …
Excerpt
nes Hjubelis ir Vizelis ištyrė tik nedidelę regos žievės neuronų skaičiaus dalį. Procentai skai- Čiuoti nuo bendro ištirtų neuronų kiekio. Tačiau apkritai neuronų pasiskirstymas trijose regos Zz0- nose sutampa su faktais, gautais regos sistemos …
Excerpt
jos ypatumą, kurį aptiko Hjubelis ir Vizelis, o vėliau ir kiti mokslininkai. Mes turime omenyje regos Žievės neuronų išsidėstymą kolonėlėmis. Štai ką apie tai rašo pats Hjubelis (1974 "res - dami įvairiomis kryptimis elektrodą į žievę, kai kada po daugelį …
Excerpt
79 pav. Regos žievės neuronų, turinčių na=- šias savybes, kolonėlės (Fjubelis, 1974). Linijos A ir B - mikroelektrodo trekai. Skersi- nės linijos vaizduoja registruotą neuronų recep- tyvinių laukų orientaciją. Kol elektrodas ėjo stat- menai Žievės …
Excerpt
Organizmai privalo turėti du judėjimo kodavi= mo mechanizmus: 1) judėjimo radialine kryptimi (organizmo link ir nuo jo) ir 2) judėjimo tan- gentine kryptimi (objekto judėjimo kryptis visą laiką statmena radialinei krypčiai ). Visos kjtos judėjimo kryptys …
Excerpt
mas yra neefektyvus. Panašiai ir su judėjimu. Kitame poliuje yra labai staigus, nedidelės truk - mės kitimas. Per trumpą laiką sistemą nespėja sureaguoti. Tokia situacija susidaro, kai regė- jimo lauke objektas juda labai greitai (pavyz- džiui, kulka). …
Excerpt
12 lentelė. Objekto judėjimo pojūčių slenks- čiai (Kostelianec ir Leušina, 1971). Objekto judė — inklainės dirginimo Maksimalus ab- soliutus slienks - tis Skyrimo slenks — tis Diferencinis slenkstis Ivairios są- lygos Šimultaniš - kai judant dviem ob- …
Excerpt
(akys tuo metu atlieka šuoliuką). Yra du tokio aiškinimo variantai. Vieną, vadinamąją aferentinę teoriją, pasiūlė Šeringtonas. Dėl akių raumenų susitraukimo aktyvuojami šiuose raumenyse esan- tys proprioreceptoriai. Aferentiniais nervais pro- …
Excerpt
me pačiame paveiksliuke pavaizduoti objektų sta- bilizavimo mechanizmai pagal H. Helmholco eferen- tinę teoriją (cit pagal Gregorį, 1970). Helmholcas teigė, kad objekto judėjimo signalus slopina ne aife- rentiniai akių raumenų signalai, o eferentiniai …
Excerpt
81 pav. Triušio viršutinio dvikalnio neuronas, selektyviai reaguojantis į objekto judėjimą iš kairės pusės apačios į dešinės pusės "viršų (Makilvainas ir Biuzeris, 1968 j. Centre ženklais "+" ir pavaizduotas recep- tyvinis laukas. 1 - 8 - reakcijų, judant …
Excerpt
mos aukštuose rasti neuronai, selektyvūs judė- jimo greičiui. Daigi visus judėjimo detektorius ga- lima suskirstyti į dvi grupes: krypties ir greičio (Ketleris ir bendraaut, 1973; Ketleris ir Purtu- lytė, 1974; Aeksejenka ir bendraaut.,, 1976 ). Judėjimo …
Excerpt
stelės,. Bet tuo metu objektas pasislenka. Jaudi- namas naujas, dar neužslopintas bipoliaras. To- dėl ganglijinė ląstelė praktiškai jaudinama tol, kol objektas juda visu receptyvinio lauko paviršiumi, Kitos ganglijinės ląstelės gauna signalus nuo ki- taip …
Excerpt
tinimą, Monokulirį erdvinį regėjimą ir Lt.) galima rasti atitinkamuose psichologijos ir fiziologijos lei- diniuose (Gregori, 1970, 1972; Koganas, 1971). Normalų binokulinį regėjimą apibūdina du reiš- kiniai: stebimo objekto projekcijų susiliejimas (itu- …
Excerpt
np Ip W o „1 | 5 į £ 7 / I N "B | / X 4 "E C M . Į „M S / 2 N / 4 1 1 / d , NM . 7 NSA / ' / X 117 VI) 2 | V 1 MV / 83 pav. Horopteris (Koganas, 1971 2. 1 —- Miulerio "teorinis" horopteris; 2 - Heringo "empirinio" horopterio vidurinė linija. Štrichuota …
Excerpt
pia abi akis, pasuka galvą. Pasukimo, Ly. rau= menų įtempimo laipsnis signalizuoja apie objekto lokalizaciją stebėtojo atžvilgiu. Nustatyti objekto kryptį padeda ir kiti išorės Objektai Čionas . Gilumos ir objektų tūringumo suvokimą įgali- na binokulinis …
Excerpt
Pokiems gyvūnams labai svarbi tiksli erdvinė orientacija: ataka turi būti tiksli, reikia sugebėti išskirti auką iš kitų o»jektų, numatyti puolimo kryptį, atstumą ir trajektoriją. Tokią vizualinę veiklą realizuoti ir įgalina binokulinis regėjimas, Tiesa, …
Excerpt
numo pavardę). Pradėjus dvejintis vaizdui, iš- nyksta sinergiška abiejų regos kanalų veikla ir prasideda jų konkurencija - binokulinis lenktynia- vimas, Vienu metu dviejų vaizdų negalima matyti. mogus mato vaizdą pakaitom tai vienoje, tai ki= toje akyje. …
Excerpt
mas. Bernso (1969) duomenimis, regos žievės neuronai atlieka abiejų tinklainių identiškų taškų sumavimą. Pavyzdžiui, regos žievės neutronas yra ribos tarp šviesaus ir tamsaus detektorius. Maksimalia reakcija tokia ląstelė atsako, kai ri- bos projekcijos …
Excerpt
nizmus, Bleikmoras (1973) nurodo, kad binokuli- nio regėjimo mechanizmų modeliai turi atitikti to- kius tris reikalavimus. 1. Modelyje turi būti neuronų, sumuojančių abiejų tinklainių identiškų taškų jaudinimus. To- kie neuronai gali būti specializuoti …
Excerpt
84 pav. Bleikmoro (1973) stereosko- pinio regėjimo neu=- roninis modelis (schema truputį modifikuota ). Šoninio kelinio kū- no monokuliniai neuronai prima informaciją iš taš- kų A ir B. Du bi- nokuliniai regos žievės mMeuronai yra taškų Air B detektoriai. …
Excerpt
AK | stiprintuvas 85 pav. Gilumos (disparatiškumo) detektorius katės regos žievėje (Bleikmoras, 1973), Šio neurono receptyvinis laukės sudarytas iš tinklainių koresponduojančių taškų, todėl jis ap- tinka objektą, sutampantį su atitinkamu horopte - rio …
Excerpt
impulsų generaciją, jaudinimo ir slopinimo pasi- skirstymą ir pan. Regos centruose yra speciali- Zuoti neuronai - detektoriai, kurių specifiškas*“ (adekvatus ) stimulas yra atitinkamas stimulo po- Žymis; orientacija, judėjimo kryptis, padėtis erd- vėje ir …
Excerpt
dividualią patirtį, detektoriai (namo, kuriame aš gyvenu, Mano pažįstamo Jono ir pan, J). Maždaus taip samprotavo neseniai miręs Žymus lenkų neu- rofiziologas Konorskis (1970), pasiūlęs gnos- tinių neuronų koncepciją. Štai ką apie tai rašo pats …
Excerpt
galima regėjimo "aiškinti" šoninio kelinio kūno ar žievės atskiros neuronų grupės elgesių lygiai taip pat, kaip negalima suprasti popierių gami- nančio fabriko veiklos iš staklių, paverčiančių rąstus piuvenomis, darbo. Dakhartiniu metu mes ti- riame, …
Excerpt
nė skaidula, pasiekusi žievės 17 lauką, sudaro kontaktus su 5-10 tūkstančių neuronų. Vieno kvadratinio milimetro piūvyje galima priskaičiuo- ti iki 25000 ateinančių ir 75000 išeinančių nervi- nių skaidulų. Šimtus ir tūkstančius kontaktų žie- vės neuronai …
Excerpt
4) atminties pėdsakų aktualizaciją; (prisiminimą, atgaminimą, atpažinimą ); 5) haliucinacijas ir ki- tus su regimuoju suvokimu susijusius reiškinius. Iš dalies tokius reikalavimus atitinka Kirvelio ir Vanago (1973, 1974, 1976) regos sistemos funk- cinės …