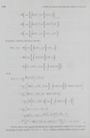Excerpt
114 8. Tiesinės stochastinės diferencialinės lygtys Ją galime interpretuoti kaip Voltero integralinę lygtį, kai duota funkcija B,, + > O, ir spręsti funkcinės analizės metodais kiekvienai konkrečiai stebimai Brauno judesio tra- jektorijai. Jei mums ypač …
Excerpt
8.10. 8.11. 6. Tiesinės stochastinės diferencialinės lygtys 115 gautojoje sprendinio X išraiškoje negali būti dalybos iš nulio; be to, galime ir tiesiogiai patikrinti, kad šia formule apibrėžtas atsitiktinis procesas iš tikrųjų tenkina Ferhiulsto lygtį. …
Excerpt
116 6. Tiesinės stochastinės diferencialinės lygtys F'(Z,) = X,. Todėl pritaikę Ito formulę (6.12 teorema) gauname 1 1 Ne Xo+ Jr "ZAlaz +5 [r zdia 0 0 J A J dZ, + 5 [ka 0 1 3 k d(Y), 4 +5 [kat 0 E L Jau Ip r ] 8.12. Teiginys. Jei Y ir Z yra du Ito …
Excerpt
8.14. 6. Tiesinės stochastinės diferencialinės lygtys 117 Teorema. Tarkime, kad H ir Y yra Ito procesai, Yo = O. Tada (464) lygties sprendinys yra 1 X, = Šy(Y), = st | e Įstnsata Žž 20 * 0 Įrodymas. Pasinaudosime diferencialinių lygčių teorijoje žinomu …
Excerpt
118 8. Tiesinės stochastinės diferencialinės lygtys 8.15. Išvada. Tarkime, kad H yra tolydus suderintas procesas, 0 Y - Ito procesas, Yg = O. Tada (+) lygties sprendinys yra I X, = Sy(Y): = H, + S(Y), Įsvonsatr = (MU s 0 Įrodymas. Pažymėkime Z, = X, — H,. …
Excerpt
8. Tiesinės stochastinės diferencialinės lygtys 119 Jei X) > Yo ir blt, x) > c(t, x) su visais t > 0, x € IR, tai beveik tikrai X, > Y, su visais t 2 O. Jei Xo Z Yo ir blt, x) > c(t, x) su visais t > 0, x € IR, ir bent vienos iš lygčių koeficientai …
Excerpt
120 8. Tiesinės stochastinės diferencialinės lygtys Figūriniuose skliaustuose esantį procesą išreikškime taip: 1 V. := X — Ja T Jews dH, 0 I = Xo — Yo + Įeuyik. ds 0 1 = Xo — Yo + [k dA,; 0 čia A, := J5E(N);!ds, t > 0, - nemažėjantis procesas. …
Excerpt
121 9. SDL sprendiniai kaip difuziniai Markovo procesai I can feel guilty about the past, apprehensive about the future, but only in the present can I act. Aš galiu jaustis kaltas dėl praeities suvokdamas ateitį, bet tik dabartyje aš galiu veikti. Abraham …
Excerpt
122 (4 9. SDL sprendiniai kaip difuziniai Markovo procesai Bendruoju atveju Markovo procesą galima apibrėžti taip: atsitiktinis procesas X vadinamas (realiuoju) Markovo procesu su perėjimo tikimybe P(s,x,t, B) …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 123 Iš čia gauname, kad (+) lygybės dešinėje esantis sąlyginis tankis (kai X — B) PijiB,, „BipB, „Bs (YIT Aa ks X) Bilistos aks LE a) D.(čis 255 AEL EG GD ooo ILO) Plika Jolita 11142 —X1)-P(K— Ik 1 XX …
Excerpt
124 9.2. 95: 9. SDL sprendiniai kaip difuziniai Markovo procesai Teiginys. Su visais t > s M — B b.t. (+++) Pastaba. Tai dar vienas Markovo savybės formulavimas — procesas X? bet kokiu laiko momentu s prasideda iš naujo nuo proceso reikšmės X* momentu s …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 125 9.4. Teiginys (difuzinio proceso Markovo savybė). Su kiekvienu x € IR procesas X* yra Markovo procesas ir su visomis aprėžtomis (mačiosiomis) funkcijomis f:1R — IR E(f(X:)IXr Xi Xi X) > B(/ (XI )IXS) …
Excerpt
126 1 9.6. 9. SDL sprendiniai kaip difuziniai Markovo procesai Toliau paprastumo dėlei nagrinėsime homogeninius (laike) difuzinius procesus X = (X*), ty. tarsime, kad (7) lygties koeficientai nepriklauso nuo laiko: 5 = b(x), oc = o(x), x € IR. Tada 9.3 …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 127 Įrodymas. Pažymėkime g(x) = b(x) f (x) + žo?(x) f" (x). Remiantis Ito formule, I AE) = 06) + [raiaks + 1 o I I = JA63)) + Įslkijas + [or (aijan, 20) 0 0 Imdami vidurkius, gauname I I B/(X) = f(x) +B …
Excerpt
128 9. SDL sprendiniai kaip difuziniai Markovo procesai 2. Dynkino formulė yra teisinga ne tik su fiksuotais laiko momentais 7, bet ir stabdymo momentais T (kurie apskritai yra atsitiktiniai). Priminsime, kad plati tokių momentų klasė yra pirmojo patekimo …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 129 Įrodymas. Remiantis Dynkino formule, egzistuoja d ae) ON) — I AAVi (GA) 11-80 5 ; T T „Af (x) 02-16 R Kita vertus, du(t X) pp Tas (a) > TS (0) orus S = Li 2 2 AO) Au(r, x). A 9.10. Pastabos. 1. …
Excerpt
130 9. SDL sprendiniai kaip difuziniai Markovo procesai arba trumpai — | PE Arlis | ro)dy=0; 01 IR čia apatinį indeksą x prie operatoriaus A užrašėme norėdami pabrėžti, kad jis taikomas kintamojo x atžvilgiu. Kadangi lygybė yra teisinga visoms funkcijoms …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 131 yra lygties dalinėmis išvestinėmis 2s — Av 1 gV 01 sprendinys, tenkinantis pradinę sąlygą v(0, x) = f(x). Įrodymas. Pirma įsitikinsime, kad funkcija v yra diferencijuojama / atžvilgiu. Pažymė- kime: …
Excerpt
132 9. SDL sprendiniai kaip difuziniai Markovo procesai ao Aris 52) i —- Y= 2 Bless I J) i (X) ž Remiantis vidurkių iteracijos taisykle, 1 Eu(t, X*) = Blog | Įatsinas sti) 0 -E(eo| f g(X: dalia i) r ž plz es |- įsta!) Ev(: < ult, AŽ ji BAU AO 7 Ia “L (Zi …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 133 kalba. Panašiai ta kalba galima užrašyti lygybę 07; f/01 = T,Af. Pažymėkime A* tiesinį operatorių, formaliai jungtinį difuzinio proceso (X*) generatoriui A, apibrėžiamą lygybe > i / ili , " A f(x) = …
Excerpt
134 9. SDL sprendiniai kaip difuziniai Markovo procesai 9.14. Teiginys (tiesioginė Kolmogorovo lygtis perėjimo tankiui). Tarkime, kad difuzinio pro- ceso |X*) koeficientai b.oc € CŽ(IR), o jo perėjimo tankis p = p(t.x,y), t > O, x.y € IR, yra tolydus …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 135 Čia A(r) ir A*(r) — operatorių A ir A* analogai, priklausantys nuo laiko parametro / (apatinis indeksas x arba y rodo, kurio argumento atžvilgiu jis taikomas): AD) —5( O) (ee)IES so oo S R A*(1) f …
Excerpt
136 9. SDL sprendiniai kaip difuziniai Markovo procesai Šią lygybę galima interpretuoti taip: jei difuzinio proceso X pradinė reikšmė X; yra atsitiktinis dydis Xg su tankiu pg, tai difuzinio proceso reikšmės X, turi :4 patį skirs- tinį su tankiu pg visais …
Excerpt
9. SDL sprendiniai kaip difuziniai Markovo procesai 137 Matome, kad išėjęs iš bet kokio taško intervale (—7/2, 7/2) šios lygties sprendinys lieka tame intervale visą laiką. Tokioje situacijoje prasminga kalbėti apie stacionarųjį tankį intervale (a, b). …
Excerpt
138 9. SDL sprendiniai kaip difuziniai Markovo procesai x € (a,b). Padauginę abi lygybės puses iš po(x) ir suintegravę pagal x < (a,b), gauname arba = b 3 AE Pol») f (x) dy = | par) dy. a a Kairioji lygybės pusė lygi nuliui, o dešinioji — integralui L …
Excerpt
9.20. 9. SDL sprendiniai kaip difuziniai Markovo procesai 139 su atsiskiriančiais kintamaisiais. Jos bendrasis sprendinys yra 2 | Ža au) v € (a,b); g(y) = N exp > čia c — bet koks fiksuotas intervalo (a, b) taškas. Iš čia ir gauname stacionariojo tankio …
Excerpt
140 10. Pavyzdžiai The most painful thing about mathematics is how far away you are from being able to use it after you have Iearned it. Skausmingiausia matematikoje yra tai, kad, ją išmokę, jūs esate dar labai toli nuo galimybės ją pritaikyti. James R. …
Excerpt
10. Pavyzdžiai 141 vaizdžiau matyti sprendinių elgsenos priklausomybė nuo parametrų (dažniausiai — nuo triukšmo intensyvumo), nes „atsitiktinumo“ įtaka visoms lygtims, priklausančioms nuo parametro, yra identiška. Todėl tų pačių lygčių su skirtingais …
Excerpt
142 10. Pavyzdžiai lėtai artėti prie —o0, kai x — +00. Tai galima interpretuoti taip: tam, kad proceso X* tikimybinė elgsena laikui bėgant stabilizuotųsi, reikia, kad jam „per daug nutolus“ nuo koordinačių pradžios jis būtų pakankamai stipriai stumiamas …
Excerpt
10. Pavyzdžiai 10.1 pav. Funkcija f(x) 4x3 — x? 1 5x drjos potencialas U. Grįžkime dabar prie stacionariojo tankio. Proceso su adityviuoju triukšmu stacio- narųjį tankį galime užrašyti Po(x) = Nexp | — SU). Matome, kad stacionariojo tankio maksimumo …