Excerpt
0.9. 0.10. 0.11. 0. Įžanga. Pagrindinės tikimybių teorijos sąvokos Sąvokas, susijusias su atsitiktinių dydžių sekų konvergavimu kvadratinio vidurkio prasme, patogu nagrinėti vadinamosios L? normos terminais. Atsitiktinio dydžio X L? norma vadinamas …
Excerpt
0.12. 0. Įžanga. Pagrindinės tikimybių teorijos sąvokos 25 |f,| < g. n e IN. Žinoma, čia turima mintyje, kad visos funkcijos f, yra apibrėžtos (ir mačios) aibėje su matu, kurio atžvilgiu ir yra imami integralai; funkcija g yra vadinama mažoruojančia sekai …
Excerpt
26 0. Įžanga. Pagrindinės tikimybių teorijos sąvokos 0.13. Atsitiktiniai procesai. Apibendrinant atsitiktinio dydžio sąvoką, galima nagrinėti at- vaizdžius (funkcijas), apibrėžtus elementarių įvykių erdvėje O ir įgyjančius ne realias reikšmes, o reikšmes …
Excerpt
11 27 1. Brauno judesys The modern mathematician has been sitting down like an Epicurean god, far from space and time, calling for chaos to play with. He gives a few brief orders and watches universes grow. Šiuolaikinis matematikas sėdi sau, kaip …
Excerpt
28 1. Brauno judesys Matome, kad su dideliais 7 sekos nariai X,„, padauginti iš atitinkamo normuojančio dau- giklio 1/,/n, yra apytikriai pasiskirstę kaip normalusis atsitiktinis dydis £ — N(0, 1). O kaip galėtume apibūdinti visos atsitiktinių dydžių …
Excerpt
1. Brauno judesys 29 proceso. Kitaip tariant, ar galima vienoje tikimybinėje erdvėje (0, £ „P) sukonstruoti tokį atsitiktinį procesą B,, t > O, kad su visais t > O turėtume X? - B, n> 007? Prieš atsakydami į šį klausimą, nubraižykime X“, / > O, grafikus …
Excerpt
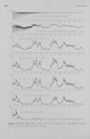
30 x16 | 1. Brauno judesys 1.1.5 pav. X?? trajektorija. 128 X, 2 ų A Ak 1 ; AL US „6 L A ikRi J a p KB 107 iš 8 10 £ $ m | 4 k vi =? 1.1.7 pav. X!28 trajektorija. SE is i ją 44 2 0 eis IZ] es 1 i 2 [ o į L A į Ly į o i S " KT 03 ti ši BIT T T 0 jų Ti T - …
Excerpt
aš) 14. 1. Brauno judesys 31 Šios teoremos neįrodinėsime, nors ir sakoma, kad pagrindinis Brauno judesio teo- rijos rezultatas yra jo egzistavimas. "Tačiau pasinaudosime ja, įrodydami pagrindines Brauno judesį charakterizuojančias savybes. Teorema (Brauno …
Excerpt
3 1. Brauno judesys Įrodymas. 1) Iš pradžių pateiksime įrodymo idėją. Su kiekvienu A > O pokytis B; — B = N(O,h) ir todėl (B44 — B,)/h — N(O,h-!). Kadangi santykio (B+, — B,)/h dispersija h“1 — oo, kai h — O, tai šis santykis negali turėti ribos, kai A — …
Excerpt
1. Brauno judesys 33 sąjunga. Todėl pakanka įsitikinti, kad P( Bx,„„) = O su visais k, m e IN. Kadangi [nT] i43 PU5E2) < P(U ( ai i=1 j=i+1 kai n > m, tai savo ruožtu pakanka įrodyti, kad su visais k € IN [nT] ISI P(U n A,)> 0 aną U— ij Kadangi įvykiai Ai …
Excerpt
34 1. Brauno judesys 1-5: (Intuityviai šis faktas gana akivaizdus, tačiau nėra trivialus ir yra atskiras daug bendres- nės Brauno judesio stipriosios Markovo savybės atvejis.) Tiksliau tariant, atsitiktiniai dydžiai B 17 kai T, 2 (B= Been = | G] kaili — 7 …
Excerpt
1.6. EA 1. Brauno judesys 35 Teiginys. Jei X < Zf,, tai X IL B; — B,,s Zu 2 t. Įrodymas. Atsitiktinių dydžių klases Zf, apibrėžėme daugiau intuityviai. Norėdami į51- tikinti teiginio teisingumu, turime tiksliau apibūdinti atsitiktinius dydžius, …
Excerpt
36 1.8. 1. Brauno judesys 2 pastaba. Atsitiktinių dydžių klasę Jf; galima apibrėžti ir visiškai griežtai. Pažymė- kimekZ— TB o-algebrą o(B;, s < r), generuotą visų atsitiktinių dydžių B,.s < t, ir visų nulinės tikimybės įvykių. Kitaip tariant, 7; yra …
Excerpt
1. Brauno judesys A B) Bš 2 2 l l 0 T Tala“ E T T 0 T T AarfĄ T T 2 Šš OF 2 4 TU 8 10 / ži si 9 2 1.2.2 pav. B“ trajektorija. 1.2.3 pav. B* trajektorija. BS | R 1 [vų | ; Jų | T WJ jr MV S S —9) 4 S Koja a 7 *54, 2 1.2.4 pav. B!“ trajektorija. 1.2.5 pav. …
Excerpt
38 1. Brauno judesys š i r I V 1.2.8 pav. B?““ trajektorija. 1.2.9 pav. B?!? trajektorija. 6 6-4 2 - 54 54 ž 44 42 5 £ 3- - 2 3- Ė š š i kų E = „a Ža z 25 a 0 L Ė 2 din AA SA 2 34 i E E i Ž i —5 Ą —5 9 6 OB 6 4 74 A E Elė 1.3 pav. B" ir n" trajektorijos, …
Excerpt
1. Brauno judesys 39 Taigi realią prasmę turi ne baltasis triukšmas, o tik jam artimi procesai. Frazę „procesas 1, yra artimas baltajam triukšmui“ reikia suprasti kad procesas B, = | 1; ds yra artimas Brauno judesiui. Norint sukurti kokio nors realaus …
Excerpt
40 2. Stochastiniai modeliai su Brauno judesiu ir baltuoju triukšmu A theory has only the alternative of being right or wrong. A model has a third possibility: it may be right, but irrelevant. Teorija turi tik vieną alternatyvą — būti teisinga arba …
Excerpt
2. Stochastiniai modeliai su Brauno judesiu ir baltuoju triukšmu 41 poveikį, turėtume įvesti pataisą — tą poveikį atspindinčią didėjančią teigiamą funkciją A (kuo didesnė populiacija, tuo aktyvesni plėšrūnai! ), ir tada lygtis galėtų atrodyti taip: X ys …
Excerpt
42 2. Stochastiniai modeliai su Brauno judesiu ir baltuoju triukšmu kurios sprendinys, kai 0 < x < M, yra Mx NC ZTS ES 2-0! Nors istoriškai iš pradžių Ferhiulsto lygtis buvo išvesta populiacijos augimui aprašyti, vėliau paaiškėjo, kad ji aptinkama ir …
Excerpt
2. Stochastiniai modeliai su Brauno judesiu ir baltuoju triukšmu 43 Šios lygties jau negalima pakeisti diferencialine lygtimi, nes, kaip minėta (1.4 teo- rema), Brauno judesio trajektorijos yra nediferencijuojamos. Tačiau ši lygtis turi prasmę kaip …
Excerpt
44 2. Stochastiniai modeliai su Brauno judesiu ir baltuoju triukšmu 2.2. Tolydusis laikas. Tas pačias lygtis galima gauti ir nagrinėjant kai kuriuos tolydaus laiko modelius. Pradėkime nuo diferencialinės lygties AX. — DO XX. kuri ekvivalenti integralinei …
Excerpt
2. Stochastiniai modeliai su Brauno judesiu ir baltuoju triukšmu 45 arba X: = bj (Xi st) +> 0(X, tr, O Perėję prie integralinio užrašo, gauname lygtį I I Nu V + [balsas + [alkusjas, 0 0 Panagrinėsime kelis pavyzdžius. Augimo lygtis. Anksčiau minėta lygtis …
Excerpt
46 3. Stochastinis integralas Brauno judesio atžvilgiu Nature laughs at the difficulties of integration. Gamta juokiasi iš integravimo sunkumų. Pierre-Simon de Laplace Ankstesniame skyriuje aptarėme, kodėl, norint suteikti prasmę stochastinėms di- …
Excerpt
0.4. 10. Pavyzdžiai 147 ekstremumo taškais. Pastaruosiuose iol EEB "A 1 Fx)=oža(x)e' (x) = 0: Ši paprasta lygtis labai svarbi triukšmo indukuotų virsmų — stacionariojo tankio ekst- remumų kokybinių pokyčių — tyrimui. Stratonovičiaus lygties atveju, …
Excerpt
148 10. Pavyzdžiai 2 N Nu“ už Polx) = => 6 |2 | —72— du] 1 x = a50|2 | (Z7- => )au] 1 o 5 (Žma - 6 — 1)| = N exp(2/02)x2H/0*-2 eXp E 0 — Nx2Mo“-2 exp |-Ž | o čia paskutiniame žingsnyje pastovų (nepriklausantį nuo x) daugiklį N exp(2/02) vėl pažymėjome N. …
Excerpt
10. Pavyzdžiai 149 /2.), taip pat turime triukšmo indukuotą virsmą. Šiek tiek mažiau juntamą kokybišką skirtumą (kurį taip pat galėtume pavadinti virsmu) stacionariojo tankio pg elgsenoje taško x = O aplinkoje galime įžiūrėti tarp atvejų Žž) o 1 no Ža. …
Excerpt
150 10. Pavyzdžiai 1 2 3 4 5 6 7 8 9 10-11 12 13 14 I X, 2 1 x | 2 3 4 5 6 7 8 9 10 11 12 13 14 I Į 21 ži …
Excerpt
10. Pavyzdžiai 151 taikymų ir kitose srityse. Pavyzdžiui, ji aprašo tam tikras chemines reakcijas, kuriose dalyvauja dvi medžiagos, ir X, reiškia vienos iš jų santykinį kiekį laiko momentu 7.4 Laikydami, kad parametras A yra veikiamas triukšmo …
Excerpt
152 10. Pavyzdžiai Toliau paprastumo dėlei nagrinėsime atvejį + = 1/2. Stacionarusis proceso tankis turi pavidalą (žr. 9.20.1 pastabą) N Day Au) Po(X) = ————— ex | ——————- x(1 — x) g2 už(1 — u)2 1/2 du) 6 -- X) i 2 | ---—— 2 --— du) 1/2 5555] Nesunkiai …
Excerpt
10. Pavyzdžiai 153 kad, kai 07 = 4, mes turime triukšmo indukuotą virsmą. Grįždami prie cheminės re- akcijos interpretacijos, įsivaizduokime, kad viena reakcijoje dalyvaujanti medžiaga yra mėlyna, o kita geltona. Kai triukšmo nėra arba jis mažas, tai …