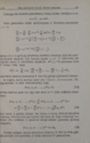Excerpt
* $ 20. Diterencialinių lygčių sistemų sprendinių egzistencija 151 yra tolydinės visų savo argumentų aižvilgiu ir patenkina sąlygą Įx—a|- k (065 Yi Ya Y.) — Ja(X5 Yu Ya = 7) S < max |Y;—7;|> (27) AO tai lygčių sistema (1) turi intervale L b |+7—a| Y€ V …
Excerpt
+ 152 VIII. Diferencialinių lygčių sistemos kur M yra konstanta, aprėžianti srityje (29) iunkcijos p ir jcs išvestinių absoliutinius didumus: R 3 0 > | …
Excerpt
$ 20. Diterencialinių lygčių sistemų sprendinių egzistencija 153 telpa srityje G, o pakankamai mažoje (n4-2)-matėję kiekvieno iš tų taškų aplinkoje dalinės išvestinės 0F 0F 0F 0F 31) Oy ? Oy“ ? Dy 2 I) Oy("i) yra tolydinės savo visų argumentų atžvilgiu, …
Excerpt
154 VIII. Diferencialinių lygčių sistemos čia nenagrinėsime. Nenagrinėsime ir (30) pavidalo lygties pavienių sprendinių. Pavyzdys. Išspręsti iteracijų metodu lygtį y“ +y = Ūsu pradinėmis sąly- gomis y (0)=0, y' (0)= I. Pažymėję y:=y ir y2=y“, turime …
Excerpt
"8.21. Tolydinė sprendinių priklausomybė nuo parametro | 155 Riboje gauname sprendinį xŠ ė 2 4 va (x)= Lim Van (X) = S, + Žr arba 4 v1(4)=sinx, y„ (x) = COS x. Grįždami prie duotos lygties, turime y(x)=sin x. Lygčių sistema (36) su pradinėmis sąlygomis …
Excerpt
156 VIII. Diferencialinių lygčių sistemos Keisdami taško A padėtį hipergretasienyje Ko, tai yra keisdami to taško koordinates srityje (3), o parametro ų reikšmes segmente In —y|Sc, galime laikyti atitinkamą sprendinį ys — pradinių reikš- mių Xo, Yio, + …
Excerpt
$ 21. Tolydinė sprendinių priklausomybė nuo parametro 157 Pažymėję Co=*0 Ci=Hi0 Ca= Ya Ca = Yo ir keisdami C+ ir xo srityje (3): b Įx4—2| GTE 22 "T n), turime sprendinių (ir integralinių kreivių) šeimą M — Ve o Ga Ci CG) (V2= 15 254050 (7) Iš jos išvedimo …
Excerpt
158 VIII. Diferencialinių lygčių sistemos kai išpildytos $ 20 3 teoremos sąlygos, turi sprendinį Y=Y( X Yo Vos Yo 5 ISO), (11) tolydiškai priklausantį nuo pradinių reikšmių X4> Vos Yo ---> »V—U. Tos pačios lygties (11) bendrąjį sprendinį, ati- tinkantį $ …
Excerpt
IX SKYRIUS AUKŠTESNIŲJŲ EILIŲ DIFERENCIALINĖS LYGTYS $ 22. Kvadratūromis išsprendžiamos aukštesniųjų eilių lygtys 1. Aukštesniųjų eilių diferencialinių lygčių sprendiniai egzis- tuoja gana bendromis sąlygomis, tačiau išreikšti šiuos sprendinius baigtine …
Excerpt
160 IX. Aukštesniųjų eilių diferencialinės lygtys lygties (1) sprendinys (3) virsta š, x E š y= [af dra až J roats (4) Išvesime formulę, išreiškiančią n kartų kartotinį integralą (4) vienu paprastu integralu. Pažymėję šį integralą I-(x), turime, kai n=2, …
Excerpt
$ 22. Kvadratūromis išsprendžiamos aukštesniųjų eilių lygtys 161 Matematinės indukcijos keliu įrodysime bendrą formulę LG) = 757 [ (OE-D 46. 6 Kaip rodo lygybė (5), formulė (6) yra teisinga, esant n=2. Laiky- damai, kad ji teisinga tam tikram n ir …
Excerpt
162 ; IX. Aukštesniųjų eilių diferencialinės lygtys kuria pasinaudoję, galime parašyti Koši uždavinio sprendinį (3) su viena kvadratūra: IE Ši pr + i KO 45, ) turintį Teiloro formulės su liekamuoju nariu pavidalą. Laikant y4> VY» > VVP laisvomis …
Excerpt
$ 22. Kvadratūromis išsprendžiamos aukštesniųjų eilių lygtys 162 2. Diferencialinę lygti y) = f (yt—D), (11) pakeitimu y“—D=z, suvedame į lygtį (su atskiriamais kintamai- siais) = =f(2), kurios sprendinys, kai f(z)Z0, yra dz | T) =x*1+C1 (12) ir, įstatę …
Excerpt
$ 22. Kvadratūromis išsprendžiamos aukštesniųjų eilių lygtys 165 2 pavyzdys. Rasti lygties y“21+y72=1 bendrąjį sprendinį ir ištirti, ar lygtis neturi dar kitų sprendinių. Parašome duotą lygtį (14) pavidalu: y =sints 94 — cost Panaudoję lygybę dy“ = y“ dx, …
Excerpt
166 IX. Aukštesniųjų eilių diferencialinės lygtys Integruodami gauname y ir, prirašę x, turime bendrąjį sprendinį a 1 +—alnlt[ GO S 5 TSC Iš pirmosios lygybės išreiškę : = + < Z— “1 =“ įstatome į antrąją, Ž x—C, ta > 5 | Kiske G Integralinės linijos yra …
Excerpt
168 IX. Aukštesniųjų eilių diferencialinės lygtys Pertvarkę gautąjį energijos integralą dę |? E A (=) = 7-7 Bie (20) ištirsime tris jo atvejus: De> 2. Esant tokiam (pakankamai dideliam) kampiniam pradžios grei- čiui, dešinė lygybės pusė visą laiką lieka …
Excerpt
: $ 23. Eilės pažeminimo atvejai. Tarpinis integralas 171 Taigi, radę tarpinį integralą, suvedame duotos diferencialinės lygties sprendimą į žemesnės eilės lygties sprendimą, pažeminame lygties eilę. ę Ištirsime eilę atvejų, kuriais galima pažeminti …
Excerpt
as 23. AT Eilės pažeminimo atvejai. Tarpinis integralas 173 „Suprastinus kairėje pusėje išnyksta u, todėl pakeitimu = (8) gauname n— 1 eilės lygtį F(x 15 5-5 sa Tokiu pat būdu ieškotume sprendinių y = 0. (9) „Kairė šios lygties pusė patenkina tapatybę 1 …
Excerpt
174 IX. Aukštesniųjų eilių diferencialinės lygtys kur daugtaškis formulėje reiškia praleistą tiesinę mažesnės už k eilės y išvestinių funkciją. Formulę (12) patikriname matematinės indukcijos keliu, dar kartą ją diferencijuodami x-u ir gaudami analogišką …
Excerpt
$ 23. Eilės pažeminimo atvejai. Tarpinis integralas 175 Sujungę abu minėtus pakeitimus į vieną, turime, išreiškę X ir y: x=eš, y=ue5- Šiam pakeitimui atlikti skaičiuojame y išvestines, įstatydami m dyla d, ALpAS e = Tūx dę dx (ueš)= 7 2 4 dy > ė o ar e a …
Excerpt
176 IX. Aukštesniųjų eilių diferencialinės lygtys Eulerio teorema. Tegul n eilės diferencialinis reiškinys F(x, y, V", y", —--, Y0)) yra, kai …
Excerpt
178 IX. Aukštesniųjų eilių diferencialinės lygtys galiojančia, ir jis turi patenkinti sąlygą (17). Iš lygybės (17), istatę (A Ž S A dun į ją vietoj F reiškinį F-—- £ ir pertvarkę, gauname: EK BS 45) = LG (7-5 0 dk dx | Oy“ 2) dpsiNops dg | T ala 0 | dun - …