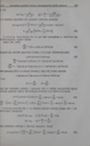Excerpt
$ 28. Eulerio lygtys 251 x*+tYvirx—V pavidalo laipsnius pakeičiame formulėse (14) ar (15) tų laipsnių realiąja ir menamąja dalimi x*cos y In x ir x“ siny In x. Panašiu būdu sprendžiame lygtį (ax +-6Y y) 1-0, (ax +-6"1y"-D1- Te, (ax1+6)y" +-0,y=0, kartais …
Excerpt
252 XI. Tiesinių diferencialinių lygčių sistemos su pastoviais koeficientais iš kur, paėmę 0;=—1, turime 02=14+i ir gauname sistemos (18) sprendinį: y= —e6+0 = — 5 (cos r L isin p), z=(1+)eGtP: = pr [tos t—sin1) L-i(cos 7 4 sin 0] ; Kitą charakteringosios …
Excerpt
$ 20. Specialaus pavidalo tiesinių nehomogeninių lygčių sistemos 253 Konstantų varijavimo išvengiame, kada yra žinomas vienas duotos nehomogeninių lygčių sistemos ar nehomogeninės lygties spren- dinys. Parodysime, kaip galima surasti tokį sprendinį, jei …
Excerpt
254 XI. Tiesinių diferencialinių lygčių sistemos su pastoviais koeficientais kur visi P„:(x) yra algebriniai polinomai. Kad galėtume parašyti vieną tokios *istemos sprendinį, turime rasti vieną paprastesnės sistemos d D a -Ta TR (R=1, 2 8) G) sprendinį. …
Excerpt
$ 29. Specialaus pavidalo tiesinių nehomogeninių lygčių sistemos 255 Panariui integruodami lygtį ir pritaikydami dešinėje pusėje inte- „ gravimo dalimis formulę, gauname lygybę, iš kurios išreiškiame „A Gpež = 02 (Aja dE = 0 a,(*) €““. Čia o (x), kaip ir …
Excerpt
256 XI. Tiesinių diferencialinių lygčių sistemos su pastoviais koeficientais kur O:(x) yra h laipsnio polinomai su neapibrėžtais koeficientais. Tuos koeficientus apskaičiuojame, įstatę sprendinio išraišką (7) į duotąją sistemą ir pareikalavę, kad gautųsi …
Excerpt
$ 29. Specialaus pavidalo tiesinių nehomogeninių lygčių sistemos 257 Jei o nėra charakteringosios lygties šaknis, tai formulėse (9) ar (11) reikia imti r=0 ir ieškoti lygties (8) sprendinio v=O0, (xe (12) pavidalo. Formulėse (11) ir (12) Gn(x) reiškia …
Excerpt
258 XI. Tiesinių diferencialinių lygčių sistemos su pastoviais koeficientais ryšiu, iš charakteringojo polinomo (17) parašome atitinkamą ope- ratorių: M=F(0):+F (0) + L A Grįžtame prie lygties (13), T laikome Ps(x)=P0+-21x+--- + 5. Tegul F(0)=0, tai yra o …
Excerpt
$ 29. Specialaus pavidalo tiesinių nehomogeninių lygčių sistemos 259 Šios lygčių sistemos determinantas, lygus savo diagonalinių ele- mentų sandaugai [F(0)]*+1, nėra nulis (nes o nepatenkina cha- rakteringosios lygties), todėl sistema turi apibrėžtą …
Excerpt
260 XI. Tiestnių diferencialinių lygčių sistemos su pastoviais koeficientais Prilyginę vienodų x laipsnių narių koeficientus, parašome koefi- cientams-g+ apskaičiuoti algebrinių lygčių sistemą | FP (0) + FUD (0) + FUD)... + FP (0)=D0 | 1 I 21. a("T)PP0)+a …
Excerpt
$ 29. Specialaus pavidalo tiesinių nehomogeninių lygčių sistemos 261 polinome, esančiame (12) pavidalo sprendinyje (šiuo atveju — me- namame), realią ir menamą dalį. Įstatę į lygtį (26) jos sprendinį (27) ir pakeitę abi lygybės puses sujungtinėmis …
Excerpt
262 XI. Tiesinių diferencialinių lygčių sistemos su pastoviais koeficientais Kada 0 nėra $ 28 (13) pavidalo charakteringosios lygties JA — DA a AO Ba Lan Dj AS AB 0 (33). šaknis, lygtis (32) turi y=* 0, (In x) 4 pavidalo sprendinį, kur O+(In x) yra ne …
Excerpt
264 XI. Tiesinių diferencialinių lygčių sistemos su pastovlais koeficientais Įstatę Koši uždavinio sąlygas (37), turime apibrėžtinę algebrinių lygčių sis- temą K — 5 44C, 4 »(0)=-2C,+C,+4C,-1=1, K0— 0-1 Gr1i=4 Apskaičiavę konstantas ir gavę C;=1, C> =0, …
Excerpt
4 - | $ 29. Specialaus pavidalo tiesinių nehomogeninių Tygčių sistemos 265 iš kur v kB GB Sa AE ir iš bendrojo sprendinio (47) parašome ieškomąjį sprendinį: : A y=y,cosar+ 20 sin at + Za (coskt —cosai)+ B 3 ks T= rų (sia EA Pin at). (48) 2 atvejis. k=a …
Excerpt
XII SKYRIUS ANTROS EILĖS TIESINĖS LYGTYS $ 30. Antros eilės tiesinių lygčių prastinimas Panagrinėsime antros eilės tiesinių homogeninių diferencialinių lygčių suvedimą į specialius pavidalus, kurie dažnai taikomi šioms lygtims spręsti ir jų sprendiniams …
Excerpt
268 XII. Antros eilės tiesinės lygtys Išsprendę šią lygtį u(x) atžvilgiu, randame: p= ži a 6) Nagrinėjamu atveju pakanka imti vieną sprendinį. Formulėje (5) imame C=1. Padauginę lygtį (1) iš gauto daugiklio u(x), turime: [rod š [PG)dx [PG dx V"1 P(x e y …
Excerpt
270 XII. Antros eilės tiesinės lygtys Funkciją u(x) parenkame taip, kad koeficientas prie z' būtų ly- gus nuliui, t. y. 2u“ (x) — “1 P(x)=0. u(x) Šios lygties bendrame sprendinyje S Ža 22 Iro dx imame C=1. Tada turime sprendinį a (17 iš kur u(x) = — = …
Excerpt
Š. 30. i Antros eilės tiesinių lygčių prastinimas 271 Nesunku įsitikinti, jog antros eilės dviejų diferencialinių lyg- čių invariantų lygybė yra būtina ir pakankama sąlyga, kad vieną iš tų lygčių (15) pavidalo pakeitimu suvestume į kitą lygtį. Kai K(x) — …
Excerpt
272 XII. Antros eilės tiesinės lygtys Įstatę pakeitimą (25) į lygtį (14), turėsime: R(x) 5 P(x) | y'=72; 1] y=ye'+2, L =y [+2+P0=+R60]=0. Padalinę šią lygybę iš y ir sutvarkę narius, tikrai gauname Rikačic lygtį: z = — [+ P6)=+ RG). (2 Taigi pakeitimas …
Excerpt
274 XII. Antros eilės tiesinės lygtys Atsižvelgę į formulę (20), turime pakeitimą 1 dx x Zz y=e E (33) kuris lygtį (31) suprastina: 4 + 1-—Ž- z=0. (34) Kai E + pakeitimas (33) redukuoja atitinkamą Beselio lygtį 1 Ay++(2-4)5=0 (35) į lygtį E z—0); kurios …
Excerpt
š 30. Svyruojaniieji ir nesvyruojantieji sprendiniai 275 n = m +. 4 pavyzdys. Išspręsti lygtį xy"—2y' 4+2xy=0. 3 (39 Šiuo atveju P(x)= — Ž. Be to, nesunku pastebėti, jog y;=x yra: duotos lygties sprendinys. Taigi, pasinaudoję formule (23), randame …
Excerpt
276 XII. Antros eilės tiesinės lygtys yra funkcijos (5) nulinės vietos. Atstumas tarp šių bet kurių abiejų T gretimų taškų yra lygus r. Be to, kiekviename intervale (a, b), kurio ilgis b-a> 7, egzistuoja lygties (2) bet kurio sprendinio bent viena nulinė …
Excerpt
$ 3t. Svyruojantieji ir nesvyruojantieji sprendiniai 277 pavidalo lygčių tyrimu, nes, kaip anksčiau matėme (žr. $ 30), pa- keitimu y=u(x)2, kur LI p no, bet kurią Po) V + PL) V B () y =0 (10) pavidalo lygtį galime suvesti į (9) pavidalą. Be to, …
Excerpt
278 XII. Antros eilės tiesinės lygtys * lo. Nenusižengdami bendrumui, šiame intervale galime imti vyi(x)> 0, nes priešingu atveju imtume sprendinį — y;(x). Turime Yi(Xo) > 0, nes y; į dešinę nuo x, didėja. Be to, y; (x4) Z0, nes prie- šingu atveju būtų …
Excerpt
$ 31. Svyruojantieji ir nesvyruojantieji sprendiniai 279 jeigu būtų, pavyzdžiui, y»(Xo) =0, tai turėtume W(xo)=0, kas prieš- tarautų Vronskio determinanto žinomai savybei. Kadangi W (x) nevirsta nuliu, tai ši funkcija yra pastovaus ženklo; leiskime, kad W …
Excerpt
280 XII. Antros eilės tiesinės lygtys ir jų atskiri tiesiškai nepriklausomi sprendiniai: AL — cos. 12 SUS (17) 21 C08217. > > SinJ+ (18) Pasinaudoję formulėmis (12) ir (13), įsitikiname, jog tarp bet kurių dviejų lygties (15) bet kurio iš sprendinių (17) …