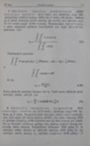Excerpt
64 Statika [II d. šias formules nevienalyčių kūnų inercijos centro koordinatėms rasti: [esa [eva [azao SC Ra Ve a G Tr 2 (2.29) [od0 [oae [ra ir inercijos centro radiusui vektoriui rasti: [rear r;=————. [ac Įeinančių į šias formules integralų integravimo …
Excerpt
IV sk.] Inercijos centrai . 65 Siuo atveju tankis o turi būti išreikštas kaip cilindrinių koordi- načių funkcija: o=o0 (r, p, z). Naudojantis sferinėmis koordinatėmis R, p, O, tūrio elementas dvu=R* sin O dR do dd, x=R sin O cos p, y=R sin O siną, z=R cos …
Excerpt
Statika [I d. Jeigu du kūno matmenys (jo storis ir plotis) yra maži, palygi- nus su trečiuoju (ilgiu ), tai tūrio elementu patogu imti to kūno dalį (2.36 brėž.) tarp dviejų statmenų jo šoniniam paviršiui plokš- tumų T; ir T;;,. Tarkime, kad tokių elementų …
Excerpt
IV sk.] Inercijos centrai 69 $ 18. Kai kurių geometrijos darinių inercijos centrai 1. Vienalytės (pastovaus linijinio tankio) tiesės atkar- pos inercijos centras yra jos viduryje, nes tiesės vidurys yra jos simetrijos centras. Todėl, jei atkarpos galų …
Excerpt
70 Statika [II d. Pusės apskritimo centrinis kampas 2a=72, todėl pusės apskriti- mo inercijos centras yra nuo centro nuotolyje 14= Ž R=0,63662R = R. 3) 4. Trikampio ABD inercijos centrui rasti (2.38 brėž.) padalijame jo plotą siaurais ruožais, brėždami …
Excerpt
72 Statika [II d. Inercijos centro atstumas nuo taško F yra - d(b + 2a) *X-- d—-0= 52 (9) Taigi taškas C dalija trapecijos vidurinę liniją FH santykiu HC +-26 TFT Via (10) Remiantis šiuo santykiu, nesunku rasti tašką C brėžimu. Pra- tęsiame trapecijos …
Excerpt
IV sk.] Inercijos centrai 73 T. Sikritiukio išpiovos (sektoriaus) ADBO inercijos centras (2.41 brėž.) yra simetrijos ašyje OD, dalijančioje centrinį kampą 40B=2a ir lanką AB pusiau. Imkime ją X ašimi. Inercijos centro abscisę (jo nuotolį nuo skritulio …
Excerpt
74 Statika [II d. ir jos inercijos centro abscisę — xc. Skritulio išpiovos inercijos centro abscisė pagal (2.25) yra ša gai E EXGE 14 ANT 5) Kadangi F;4+F= Fo, tai *o= aTa, (15) Iš (2.41) brėžinio ir iš 7 pavyzdžio turime: F,= aR?, 5— S, p— Z AB-OE= …
Excerpt
IV sk] Inercijos centrai 75 "Iš brėžinio matyti, kad R cos a; = OK, R cos a> =0OL. Todėl x0= Ž(OK+0L)=1(KL+OL+0L)=O0L+5KL. (17) Vadinasi, taškas C yra atkarpos KL (juostos aukštinės) viduryje. 10. Sukinio. paviršiais Žikercijos en tr as (2.43 brėž.) yra …
Excerpt
76 Statika ; [II d. ženklų ir suprastinti trupmenas). Taip samprotaudami pagal (2.34) formulę gauname 1 [ias š r Da, = = 2 (2.50) [inas ( Vadinasi, piramidės inercijos centras C dalija tiesę, jungiančią jos viršūnę ir pagrindo inercijos centrą, santykiu …
Excerpt
78 : Statika | "II d. Antra vertus, kreivės lanko AB inercijos centras, įstačius (2.34) iormulėje 0;=1, yra nutolęs nuo sukimosi ašies nuotoliu [a Ti Vadinasi, [xar=1c- Todėl PC 219 (2.54) Antrojoje teoremoje sakoma: sukinio, gauto sukant plokščią [i- …
Excerpt
Via] 5 Atsitiktinė jėgų sistema 79 Pagrindinė Puanso metodo teorema yra tokia: jėga F, veikianti standų kūną tiese AB, yra ekvivalenti tokiai pat jėgai, veikiančiai ta pačia linkme tiese CD, lygiagrečia AB, it vadinama- jam prijungtajam jėgų dvejetui (F, …
Excerpt
V sk.] Atsitiktinė jėgų sistema 8! lygiagretainį OCAB, kurio kraštinės yra dvejeto jėgos, galima pa- keisti lygaus ploto plokštuminiu elementu — lygiagretainiu OC“BA, —> kurio kraštinės yra jėga F ir atkarpa 04 (2.50 brėž.). Tokio lygia- —> gretainio …
Excerpt
84 Statika [II d. * = £ Tačiau mišrioji vektorių sandauga (OExF) z?=0, nes vektoriai —> — OE ir z0 yra kolinearūs (žr. 1. $ 12). Vadinasi, ME= (r xF)z7= MP. 3) Iš (1) formulės dar gauname, kad jėgos momentas ašies atžvilgiu yra lygus nuliui, kai jėga yra …
Excerpt
V sk.] Atsitiktinė jėgų sistema 85 taisykles. Pavyzdžiui, jėgos momentą koordinačių pradžios atžvil- giu galime išreikšti tokiu determinantu (1.36): i j k M“ DX E— | 2 | (2.64) LŽ I E Šio determinanto minorai, atitinkantieji vienetinius koordinati- nių …
Excerpt
86 Statika [II d. to, kuris yra ekvivalentus dinamos dvejetui ir kurio jėgų didumas yra lygus dinamos jėgai. Dinamą galima pakeisti dviem nesusikertančiom jėgom, esančiomis statmenose plokštumose. Iš tikrųjų, jėgų dvejetą (F,, 2.54 brėž. 2.55 brėž. —F;) …
Excerpt
kiai V sk.] Atsitiktinė įėgų sistema 87 rio jėgos būtų F ir —F, o momentas vektorius būtų MO ir padė- kime šį dvejetą plokštumoje O taip, kad jo petys A būtų statmenas F ir MO, taigi statmenas plokštumai P, o viena dvejeto jėgų, —F, būtų pridėta prie …
Excerpt
88 Statika [II d. $ 24. Jėgų sistemos invariantai Statiniais jėgų sistemos invariantais vadinsi- me dydžius, kurie apibūdina jėgų sistemą, nepriklausomai nuo pa- sirinktojo redukcijos centro. Pirmasis jėgų sistemos invariantas yra sisie- mos svarbiausias …
Excerpt
90 Statika [II d. ekvivalenti nuliui, t. y. visi prijungtieji dvejetai atsisveria, ir siste- ma yra ekvivalenti atstojamajai F= XF, pridėtai prie redukcijos centro. Antruoju atveju MP yra statmenas F. Kai FM=0, tai ir “ dinamos parametras p= K- EO Todėl …
Excerpt
V sk.] Atsitiktinė jėgų sistema 91 Atstojamosios padėčiai rasti patogu naudotis vadinamąja Varinjono teorema: jei jė- gų sistema yra ekvivalenti atstojamajai jėgai, tai jos momentas bet kurio taško atžvilgiu yra lygus visų apskaičiuotų to paties taško …